Shape

Shape

Measures of shape offer us an idea of what the distribution of scores looks like when plotted.

• Unimodal: one peak
• Bimodal: two peaks
• Multimodal: multiple peaks
• Rectangular distributions: multiple peaks of the same magnitude

There are two measures of shape we commonly use:

• Skewness (or simply Skew)
• Kurtosis

Skewness

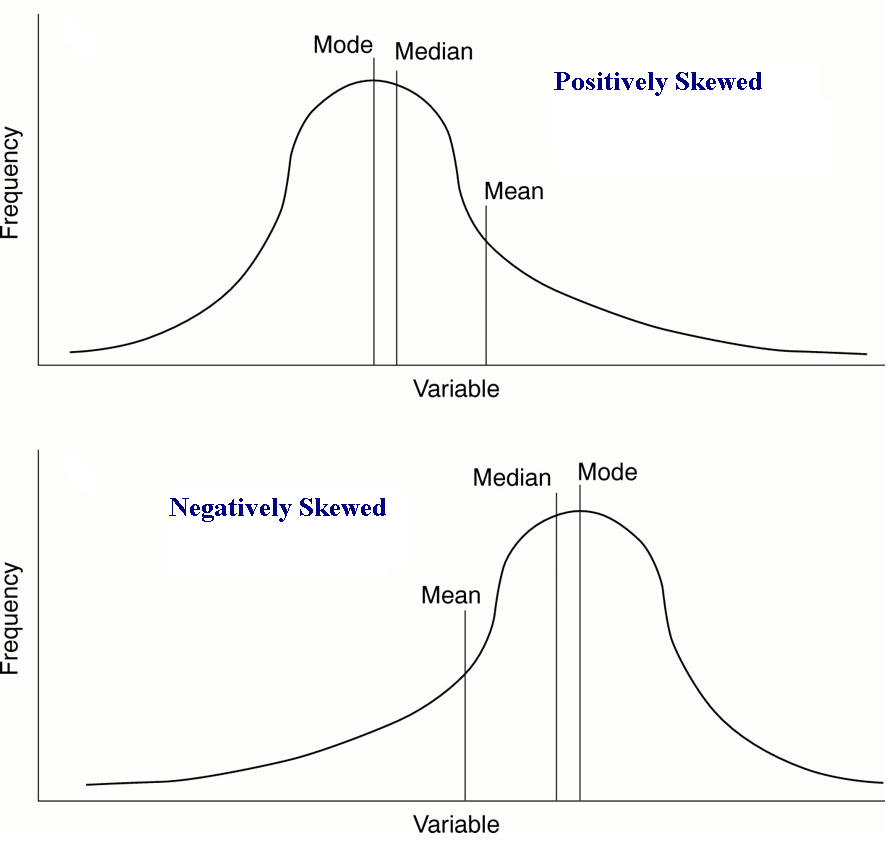
The Skewness refers to the amount of non-symmetry a distribution of scores contains.

• Negative skew is when the tail points to the smaller values and most scores are located at the larger values.
• Positive skew is when the tail points to the larger values and most scores are located at the smaller values.
• Zero skew indicates symmetry.

The farther from zero the skewness, the less symmetric the distribution of scores.

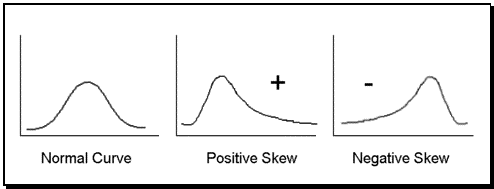
Recognizing Skewness

Recognizing Skewness

Zero Skewness Positive Skewness Negative Skewness

Kurtosis

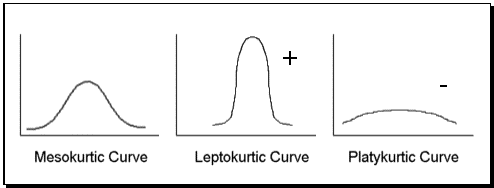
The Kurtosis measures the amount of tail magnitude, commonly referred to as ``peak-ness'' or ``flatness'' of a distribution of scores.

• Kurtosis is based on the size of a distribution's tails.
  • A distribution with a large, positive kurtosis has thin tails and the distribution looks peaked.
    • This is known as Leptokurtic.
  • A distribution with a large, negative kurtosis has thick tails and the distribution looks flat.
    • This is known as Platykurtic (like a plateau).

Recognizing Kurtosis

Zero Kurtosis Positive Kurtosis Negative Kurtosis

Describing a Distribution's Shape

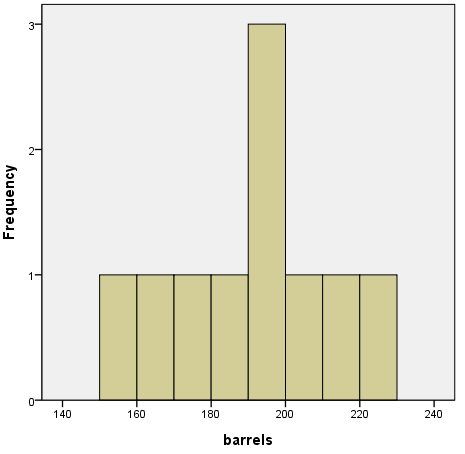
How can we describe the shape of the distribution of our sample's Barrels variable?
Unimodal.
Slightly Negatively Skewed?
Leptokurtic (positive kurtosis)?

Deceptive Sample Leads to Poor Judgment

• When we have such a small sample size (n = 10), we must be careful when eyeballing the distribution.
  • Actually, the Skewness for Barrels is .068
  • And, the Kurtosis for Barrels is -.595
• Generally, in the social sciences; we expect variables to have skewness and kurtosis between +1 and -1.
• When a variable displays a skewness or kurtosis larger than +1 or -1, then we say the variable is not symmetrical and/or does not have well proportioned tails.