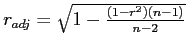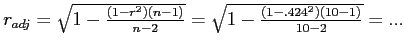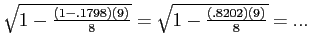


Next: Properties
Up: Classes
Previous: Shape
Contents
Relationship
- Measures of relationship offer us an idea of how two sets of scores, or two variables, are related.
- How much variance do the two variables share.
- How much does one variable overlap another.
- Measures of Association: When at least one of the two variables is ordinal or nominal in scale.
- Correlational Measures: When both variables are interval or ratio scaled (continuous or nearly so).
- For the time being, we will do a quick overview of the Measures of Association and focus more attention on the Correlational Measures.
Measures of Association
There are several Measures of Association.
- Point-Biserial Correlation (
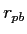 ) when one variable is dichotomous.
) when one variable is dichotomous.
- Phi Coefficient (
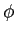 ) when both variables are dichotomous.
) when both variables are dichotomous.
- Spearman's rho (
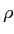 ) or (
) or (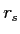 ) and Kendall's tau (
) and Kendall's tau (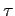 ) when one or both variables are ranked (ordinal).
) when one or both variables are ranked (ordinal).
Correlational Measures
There are three key Correlational Measures we will cover here.
- Covariance (
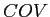 )
)
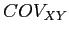 where x and y are the two variables we are using.
where x and y are the two variables we are using.
- Correlation; the Pearson Product-Moment Correlation Coefficient (
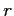 )
)
- Adjusted Correlation Coefficient (
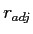 )
)
Covariance
The Covariance is a non-standardized measure of relationship; meaning it can not be used to compare the relationship of two variables to the relationship of two other variables.
- Covariance is not terribly meaningful by itself, but it is used in calculating other statistics (e.g., correlation).
- It is not terribly meaningful because, its scale or metric is determined by the two specific variables on which it is calculated.
- For this reason, it is not comparable across different pairs of variables.
What is Covariance then?
- Calculating the covariance gives us a numeric measure of the degree or strength of relationship between two variables.
- Covariance can range between
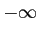 and
and 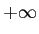
- The larger the number (negatively or positively), the greater or stronger the relationship.
- When covariance is zero, there is no relationship between the variables; virtually never happens.
- The sign associated with a covariance tells us the direction of the relationship between the two variables.
- If the sign is negative, then high scores on one variable are associated with low scores on the other variable.
- If the sign is positive, then high scores on one variable are associated with high scores on the other variable.
Calculating Covariance
The definitional formula for calculating the covariance of two sample variables (X, Y) is:
This formula is very similar to the variance formula; for instance if we swap out all the Y's in the above formula for more X's, we get the variance of X:
Computational formula for Covariance
- The computational formula is generally considered more manageable when calculating by hand.
- But; as mentioned previously with standard deviation, both the computational and definitional formulas provide the same answer.
Oil Example sample data: Covariance Calculation
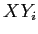 |
Barrels (X) |
Costs (Y) |
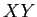 |
|
1 |
159 |
520 |
82680 |
|
2 |
166 |
570 |
94620 |
|
3 |
176 |
510 |
89760 |
|
4 |
185 |
560 |
103600 |
|
5 |
191 |
560 |
106960 |
|
6 |
194 |
530 |
102820 |
|
7 |
199 |
560 |
111440 |
|
8 |
207 |
580 |
120060 |
|
9 |
216 |
550 |
118800 |
|
10 |
228 |
560 |
127680 |
|
|
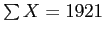 |
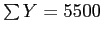 |
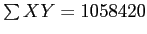 |
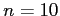
Example Calculation continued
Taking the sums and 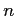 from the previous slide, we can use the computational formula to complete the calculation of covariance.
from the previous slide, we can use the computational formula to complete the calculation of covariance.
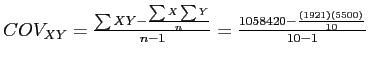 ...
...
So, the covariance of X and Y is 207.78; which does not seem terribly meaningful.
- Positive number, indicates that high scores on
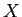 are associated with high scores on
are associated with high scores on 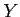 (and vice versa).
(and vice versa).
- Large number (i.e., far from zero), so the two variables are likely to be fairly well related.
- Beyond that, not much can be said.
Correlation
The Correlation (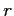 ) is a standardized measure of relationship; meaning it can be compared across multiple pairs of variables, regardless of scale.
) is a standardized measure of relationship; meaning it can be compared across multiple pairs of variables, regardless of scale.
- Correlation is the most frequently used statistic for assessing the relationship between two variables4.
- Correlation allows us to describe the direction and magnitude of a relationship between two variables.
- Correlation is very similar to covariance, indeed we use the covariance to calculate correlation.
- Correlation is used in many inferential statistics and often a matrix of correlations is the input data used to calculate them.
Interpretation of Correlation
Once calculated:
- Correlation (
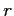 ) can range between
) can range between 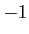 and
and 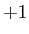 .
.
- The larger the value (positive or negative), the stronger the relationship between the variables.
- If
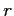 is negative, then high scores on one variable are associated with low scores on the other variable.
is negative, then high scores on one variable are associated with low scores on the other variable.
- If
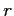 is positive, then high scores on one variable are associated with high scores on the other variable.
is positive, then high scores on one variable are associated with high scores on the other variable.
- If
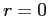 , then there is no relationship between the variables (virtually never occurs).
, then there is no relationship between the variables (virtually never occurs).
The size of 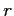 indicates the strength of the relationship and the sign (positive or negative) indicates the direction of the relationship.
indicates the strength of the relationship and the sign (positive or negative) indicates the direction of the relationship.
Calculating Correlation
Calculating correlation is quite easy, once you have the covariance.
- So, given the descriptive statistics from previous slides:
- Barrels (
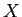 ):
): 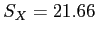
- Costs (
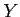 ):
): 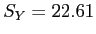
- and:
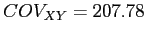
- The correlation is .424 between Barrels and Costs.
What does that mean?
The correlation between Barrels and Costs is 0.424...so what?
- We can say that Barrels and Costs are positively related.
- Meaning; high scores on one tend to be associated with high scores on the other.
- And, low scores on one tend to be associated with low scores on the other.
- But what of the magnitude? This is a bit more tricky.
- Generally, familiarity with recent, similar research will guide your interpretation of magnitude.
- Same field, topic, variables, etc.
- In the social sciences, it is common to find correlations around .400 to .600 referred to as `moderate', `good', or even `strong' (in the case of .600).
Taking Correlation a step further.
One very good way of helping yourself to interpret correlation is to square it.
- By squaring the correlation (
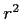 ), we can interpret it as the amount of variance shared between the two variables.
), we can interpret it as the amount of variance shared between the two variables.
- So, we can say barrels extracted and rig operating costs share 17.98% of their variance.
- Now we have a better understanding of the relationship between the two variables.
- Keep in mind:
- Squaring any correlation coefficient makes it smaller (
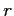 is always between -1 and +1).
is always between -1 and +1).
Adjusted Correlation
When sample sizes are small, as they are here (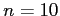 ), the sample correlation will tend to overestimate the population correlation.
), the sample correlation will tend to overestimate the population correlation.
- Meaning,
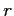 and
and 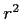 tend to be larger than they truly are in the population.
tend to be larger than they truly are in the population.
- The relationship appears stronger than it actually is in the population.
- So, we generally correct for this problem by adjusting
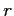 .
.
Adjusting our example correlation
Adjusting our Oil example correlation:
- Our correlation shrank from
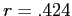 to
to
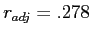
- Shared variance shrank from
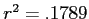 to
to
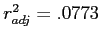 .
.
- We now have a more accurate sample estimate of the relationship between Barrels and Costs.
- They share 7.73% of their variance (i.e., clearly a
weak relationship).
Additional Considerations with Measures of Relationship
Measures of relationship tell us something about whether or not two (or more) variables share variance.
They do NOT tell us what causes the relationship!
Nor do they tell us if one variable causes another!
- You will often hear this: ``Correlation does not equal causation!''
- X may cause Y
- Y may cause X
- Z may be causing the relationship between X and Y
- Although, we do tend to use correlation (and other measures of relationship) in the process of investigating causal relationships.



Next: Properties
Up: Classes
Previous: Shape
Contents
jds0282
2010-10-04
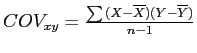
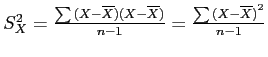
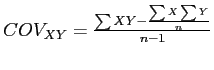
![]()
![]() from the previous slide, we can use the computational formula to complete the calculation of covariance.
from the previous slide, we can use the computational formula to complete the calculation of covariance.
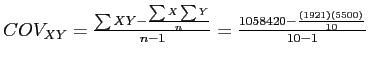 ...
...
![]() ) is a standardized measure of relationship; meaning it can be compared across multiple pairs of variables, regardless of scale.
) is a standardized measure of relationship; meaning it can be compared across multiple pairs of variables, regardless of scale.
![]() ), the sample correlation will tend to overestimate the population correlation.
), the sample correlation will tend to overestimate the population correlation.