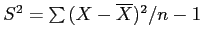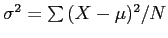
Next: Summary Up: Module 3: Describing Data Previous: Relationship Contents

Properties of Statistics

There are 4 properties we use to evaluate statistics.

Sufficiency
Unbiasedness
Efficiency
Resistance

Some of them you are already familiar with...

Sufficiency

The Sufficiency of a statistic refers to whether or not it makes use of all the information contained in a sample to estimate its corresponding parameter.

As an example, consider measures of central tendency:
- The mean is very sufficient because, it uses all the scores when being calculated.
- The median and mode are not very sufficient because, they only use one or two scores.

Unbiasedness

The Unbiasedness refers to how well a sample statistic represents its associated population parameter.

As we saw with correlation, some statistics ( 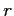$r$ ) are more biased than others ( $r_{adj}$ ).
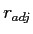Recall how we calculated:
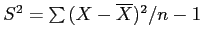
- Sample variance: $S^2 = \sum{(X - \overline{X})^2} / n - 1$
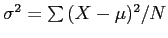
- Population variance: $\sigma^2 = \sum{(X - \mu)^2} / N$
This is due to something we will discuss more later, degrees of freedom (df).
For now, consider this: we use 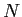$N$ in the population formula because, we have all of the scores.
When dealing with samples, we do not have all the scores (of the defined population) and we make an
adjustment, dividing by 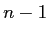$n - 1$ .

Efficiency

The Efficiency refers to how much a statistic can change from sample to sample. An efficient statistic does not change.

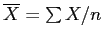
Consider the sample mean: $\overline{X} = \sum{X} / n$
If we took an infinite number of repeated samples from a symmetrical population distribution with 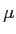in the center:
- The mean of each sample would be fairly close to 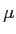$\mu$ and the mean of all those sample means would be $\mu$ .
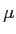The key to that statement being true is ``symmetrical population distribution with 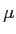in the center''.
- Extremely high and low scores (those farthest from 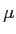$\mu$ ) are rare when compared to the number of scores near $\mu$ .
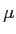- Therefore, we can expect most of those repeated samples to have a mean close to 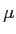$\mu$ , because most of the scores in general (in the population) are close to $\mu$ .

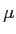Resistance

The Resistance refers to how resistant a statistic is to outliers (extreme scores).

If extreme scores do not influence the statistic, then the statistic is resistant.
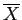
Again, consider measures of central tendency: Mo, Mdn, $\overline{X}$
Both Mo and Mdn only consider the very center of a distribution, so they are very resistant.
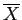$\overline{X}$ is very sensitive to outliers, they pull the mean toward them thus making the mean not very resistant.

Next: Summary Up: Module 3: Describing Data Previous: Relationship Contents

jds0282 2010-10-04