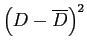


Next: Independent
Up: Module 8: Introduction to
Previous: One Sample
Contents
2.1. Dependent Samples t test
Dependent Samples t Test
- First, it goes by many names...
- Dependent Samples t Test
- Matched-Pairs t Test
- Repeated Measures t Test
- t Test for Dependent Means
- t Test for Related Samples
- Essentially, it compares two sample means which are known to be related in some way.
Types of Related Samples
There are three types of related samples which are appropriate for the Dependent Samples t Test.
- Natural Pairs: Comparing the scores of two groups of subjects which are related naturally.
- E.g., Twins (twin 1 vs. twin 2 on scores of trait anxiety).
- Matched Pairs: Pairs two groups of subjects on some characteristic that is likely to be important to the variable which you are studying.
- E.g., Married couples (husbands vs. wives on ratings of marital satisfaction).
- Repeated Measures: Same people at two different times of measure (of the same variable).
- E.g., Pretest/post test (patients' life satisfaction ratings before and after treatment for depression).
Gist: There is some sort of known meaningful relationship between the two groups of scores.
Similiar to previous tests, but...
2.2. Dependent Samples t Test Example
NHST Example
- We are interested in relationship satisfaction of young adults before and after they go off to college/university which separates them from their sweat-heart.
- Relationship satisfaction rating: 0 - 50 range, higher score indicates greater satisfaction.
- Collect a sample of young adults which are about to be separated from their boy- or girl- friend by going to college.
- Have them rate their satisfaction with the relationship.
- Then, after they have spent the first semester at colleges/universities (away from their sweat-heart), they again rate their relationship satisfaction.
Step 1: State the Null and Alternative Hypotheses
Define the populations: Relationship Satisfaction = RS
- Population 1: RS prior to college separation.
- Population 2: RS after the first semester.
State the Hypotheses:
Note the directional alternative hypothesis; pay careful attention to how we specified the hypotheses in symbols.
- If the alternative hypothesis expected an increase, then
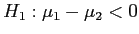 or
or 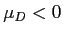
Step 2: Comparison Distribution (estimate 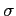 with
with 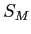 ).
).
|
Pair |
Before |
After |
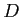 |
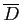 |
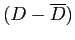 |
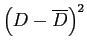 |
|
1 |
40 |
32 |
8 |
8 |
0 |
0 |
|
2 |
38 |
31 |
7 |
8 |
-1 |
1 |
|
3 |
36 |
30 |
6 |
8 |
-2 |
4 |
|
4 |
42 |
31 |
11 |
8 |
3 |
9 |
|
4 |
|
|
32 |
|
|
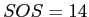 |
Step 3: Determine the critical value
Step 4: Calculate t
- Remember we are dealing with the difference scores (D) but the t formula is essentially the same as above.
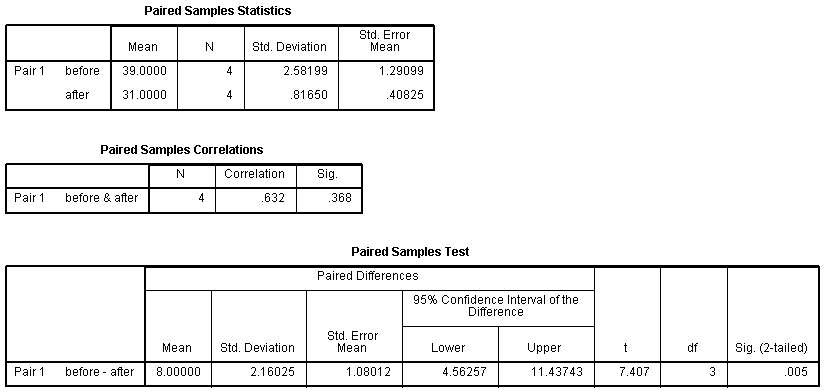
- From previous calculations, we have:
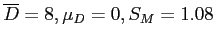
- So, our
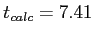 which is fairly large.
which is fairly large.
Step 5: Compare and make a decision.
- Since
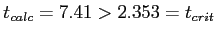 we reject the null hypothesis.
we reject the null hypothesis.
- The initial interpretation is...
There was a significant decrease in ratings of relationship satisfaction from before college separation (
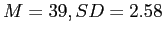 ) to after the first semester of college separation (
) to after the first semester of college separation (
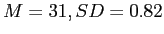 ),
),
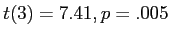 (one-tailed).
(one-tailed).
- One could also state the results as;
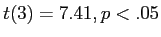 because .05 was our significance level.
because .05 was our significance level.
- The 3 above is the degrees of freedom (df).
- At this point in the course, you should be able to calculate the means and standard deviations of each group of scores; however the exact
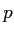 value was obtained by verifying the results above in SPSS (see below).
value was obtained by verifying the results above in SPSS (see below).
2.3. Effect Size
Effect Size
- Here, we do not know
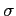 so we use
so we use 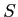 to estimate (not
to estimate (not 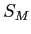 because it is influenced heavily by sample size).
because it is influenced heavily by sample size).
- Effect sizes are not influenced by sample size.
- Also, because we are dealing with difference scores, we use slightly different symbols in the formula:
Effect Size continued
- Cohen's d for difference scores:
- We have
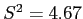 from above, which leads to an estimate of
from above, which leads to an estimate of 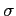 :
:
- Which in turn, leads to d:
2.4. Using Delta for Power
Using Delta ( ) for Statistical Power
) for Statistical Power
- As was done in the one sample t test situation, here again we calculate
 as a combination of sample size and effect size and use it to look up the power in the
as a combination of sample size and effect size and use it to look up the power in the  table.
table.
- However, because we now have two samples, the formula is slightly different.
- So, for our current example, we get:
- Since our
 table shows that anything with a
table shows that anything with a 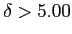 equates to power greater than 0.99, we can safely assume we have at least a power of 0.99.
equates to power greater than 0.99, we can safely assume we have at least a power of 0.99.
Using Delta  to calculate appropriate sample size
to calculate appropriate sample size
- The more useful way to use
 is for calculating adequate sample size during the planning of the study.
is for calculating adequate sample size during the planning of the study.
- First, we need to calculate
 for a desired power
for a desired power 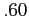 with a one-tailed test at .05 significance level.
with a one-tailed test at .05 significance level.
, now we can calculate the sample size for a given effect size 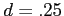 .
.
2.5. 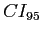
Calculating a Confidence Interval with 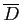
- Using essentially the same procedures we used with the one sample t test, we can calculate the lower limit (LL) and upper limit (UL).
- Recall, the general formulas for a confidence interval are: LL = (-crit)*(SE) + mean and UL = (+crit)*(SE) + mean
- When in the Dependent Samples situation, we simply use the difference score mean.
Interpretation of 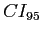
- In this example, we calculated a 95% confidence interval (
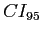 ) because our critical value was based on a significance level of .05.
) because our critical value was based on a significance level of .05.
- If we drew an infinite number of samples of young adults' relationship satisfaction ratings, 95% of those samples' difference score means would be between 5.459 and 10.541.
- Remember, the population difference score mean is fixed (but unknown); while each sample has its own difference score mean (samples fluctuate).
2.6. Summary of Section 2
Dependent Samples t Test Usage?
Fortunately...
- The Dependent samples t Test is quite powerful (i.e., statistical power).
- Repeated measures designs (or matched pairs, dependent samples, etc.) have more power due to less variance between the groups of scores.
- The same individuals being tested at different times.
- But, there is no control group for comparison, so the results are somewhat limited.
- The t test in general is robust to errors.
- Robust (in this situation) means, even with moderate departures from normality we can be confident in our results.
Summary of Section 2
Section 2 covered the following topics:
- The Dependent Samples t Test.
- An NHST example of the Dependent Samples t Test.
- Cohen's d Effect Size
- Use of delta (
 ) for Statistical Power
) for Statistical Power
- Use of delta (
 ) for calculating a-priori sample size
) for calculating a-priori sample size
- Calculation of Confidence Intervals.



Next: Independent
Up: Module 8: Introduction to
Previous: One Sample
Contents
jds0282
2010-10-15
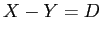 for the difference scores.
for the difference scores.