


Next: t Summary
Up: Module 8: Introduction to
Previous: Dependent
Contents
3.1. Independent Samples t test
Independent Samples t Test
- It too goes by many names...
- The Independent Samples t Test
- Independent Means t Test
- Between Groups t Test
- The t test for Independent Means...
- Essentially, it is used for comparing two sample means which are not related in some known or meaningful way.
- Two Independent groups of scores.
Methodological Application
- The Independent Samples t Test is applicable when you have a dichotomous Independent Variable (IV) and an interval or ratio scaled Dependent Variable (DV).
- One IV with two categories (sometimes called conditions).
- One DV which is continuous or nearly continuous.
- Evaluating two treatments for Schizophrenia.
- IV = Treatment (with two groups).
- Electro-Convulsive Therapy (ECT)
- Insulin Shock Therapy (IST)
- DV = Frequency of Hallucinations
Application Distinctions
- Dependent Samples t Test: two groups of scores from the same people or people related in some meaningful, known way.
- Same people at time 1 vs. time 2 or twin 1 vs. twin 2.
- Comparison distribution: Distribution of Difference Scores.
- Independent Samples t Test: two independent groups of people, each with a set of scores (i.e., group 1's scores vs. group 2's scores).
- A group of people exposed to one treatment vs. a group of people exposed to another treatment.
- Comparison distribution: Distribution of Differences Between Means.
A Quick note about notation...
- With the Independent Samples t Test, we have two groups, identified with the notation:
- Group 1:
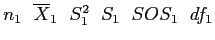
- Group 2:
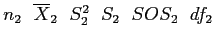
- So this:
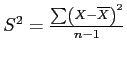 becomes:
becomes:
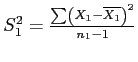 for group 1.
for group 1.
- Use subscripts to identify each group with either a 1 or a 2 subscript.
Getting to the Distribution of Differences Between Means (part 1).
- Each group has a population distribution.
- We can estimate those populations' variances with the sample variances:
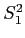 and
and 
- Each group can be used to create a distribution of means.
- We can estimate the distribution of means' variances with the sample variances divided by the number of individuals in the samples
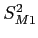 and
and 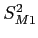
- Using those two distributions of means, we can create a Distribution of Differences Between Means.
BUT...
Getting to the Distribution of Differences Between Means (part 2).
- Because we assume both
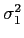 and
and 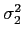 are equal; we must come up with an average of the two estimates
are equal; we must come up with an average of the two estimates 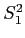 and
and  to get the best overall estimate of the population variance*.
to get the best overall estimate of the population variance*.
- *This is especially crucial when the size of each group is different.
- This best estimate is called the pooled estimate of the population variance.
- Symbol:
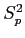
Getting to the Distribution of Differences Between Means (part 3).
- To get
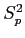 you must get
you must get 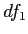 ,
, 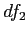 , and
, and 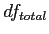 (also called
(also called 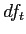 )
)
- So, then we can get
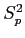 using:
using:
- But wait...there's more...
Getting to the Distribution of Differences Between Means (part 4).
- Now, we take
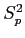 and figure
and figure 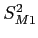 and
and 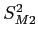 by removing the influence of sample size.
by removing the influence of sample size.
- Which leads to...the variance of the distribution of differences between means.
- Which then leads to the standard deviation of the distribution of differences between means.
Finally...the t test.
- Now that we have
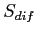 we can calculate t or
we can calculate t or 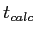
- We would then use the
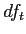 and our significance level to look in the t table to find our cutoff sample score (
and our significance level to look in the t table to find our cutoff sample score (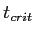 )
)
3.2. Hypothesis Testing Example
NHST Example
- Examine whether viewers of John Stewart's The Daily Show know significantly more about world affairs than viewers of Bill O'Reilly's The O'Reilly Factor show.
- Randomly sample 16 cable viewers, randomly assign them to one of two show groups; Daily and Factor.
- Have the participants watch 20 recent episodes of one show or the other, depending on their group assignment.
- Assess their knowledge of Current World Events using the CWE questionnaire, which has a range of 1 to 10.
Step 1
- Define the populations and restate the research question as null and alternative hypotheses.
- Population 1: Americans who watch The Daily Show.
- Population 2: Americans who watch The O'Reilly Factor.
- In terms of knowledge about current events.
- Notice the directional alternative hypothesis (
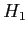 ) which indicates a one-tailed test.
) which indicates a one-tailed test.
Table 3: Daily Show Group
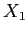 |
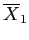 |
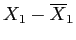 |
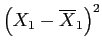 |
|
6 |
6.75 |
-0.750 |
0.563 |
|
6 |
6.75 |
-0.750 |
0.563 |
|
9 |
6.75 |
2.250 |
5.063 |
|
8 |
6.75 |
1.250 |
1.563 |
|
4 |
6.75 |
-2.275 |
7.563 |
|
6 |
6.75 |
-0.750 |
0.563 |
|
7 |
6.75 |
0.250 |
0.063 |
|
8 |
6.75 |
1.250 |
1.563 |
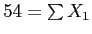 |
|
|
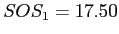 |
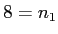 |
|
|
|
Table 4: Factor Show Group
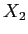 |
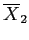 |
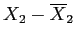 |
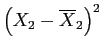 |
|
5 |
3.875 |
1.125 |
1.266 |
|
4 |
3.875 |
0.125 |
0.016 |
|
3 |
3.875 |
-0.875 |
0.766 |
|
1 |
3.875 |
-2.875 |
8.266 |
|
5 |
3.875 |
1.125 |
1.266 |
|
6 |
3.875 |
2.125 |
4.516 |
|
3 |
3.875 |
-0.875 |
0.766 |
|
4 |
3.875 |
0.125 |
0.016 |
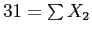 |
|
|
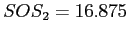 |
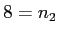 |
|
|
|
Step 2(a)
- 2. Determine the characteristics of the comparison distribution.
-
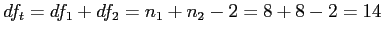
- And from above,
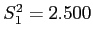 and
and 
- (a) Calculate the pooled estimate of the population variance.
- So,
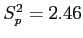
Step 2(b)
- (b) Calculate the variance of each distribution of means:
- Please note; if the groups were different sizes, the variances of each distribution of means would be different.
Step 2(c) and Step 2(d)
- (c) Calculate the variance of the distribution of differences between means:
- So,

- (d) Calculate the standard deviation of the distribution of differences between means:
- So,
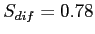
Step 3
- 3. Determine the critical sample score on the comparison distribution at which the null hypothesis should be rejected.
- Significance level = .05
- Two-tailed test (based on
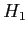 ).
).
-
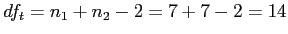
Step 4
- 4. Determine the sample's score on the comparison distribution:
- Compute
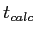
- So,

Step 5
- 5. Compare the scores from Step 3 and Step 4, and make a decision to reject the null hypothesis or fail to reject the null hypothesis.
- Because;
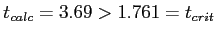 we reject the null hypothesis and conclude there was a statistically significant difference between the two show groups.
we reject the null hypothesis and conclude there was a statistically significant difference between the two show groups.
- But, you should know by now, that's not the whole story.
3.3. Effect Size
Calculating Effect Size for two Independent Groups
- Recall, the general formula for Cohen's d.
- In the current (independent groups) situation, we have:
- So, the effect size is fairly large;
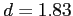
3.4. Statistical Power
Using Delta ( ) for Statistical Power
) for Statistical Power
- As was done with the Dependent Samples t Test situation, here again we calculate
 as a combination of sample size and effect size and use it to look up the power in the
as a combination of sample size and effect size and use it to look up the power in the  table.
table.
- We use the exact same formula as was used with Dependent Samples (Section 2 above).
- So, for our current example, we get the following (where
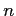 is the number per group):
is the number per group):
- The
 table shows that with a
table shows that with a 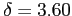 (note: it is best to round down) we have a power of 0.98.
(note: it is best to round down) we have a power of 0.98.
Using Delta  to calculate appropriate sample size
to calculate appropriate sample size
- The more useful way to use
 is for calculating adequate sample size during the planning of the study.
is for calculating adequate sample size during the planning of the study.
- First, we need to calculate
 for a desired power
for a desired power 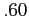 with a one-tailed test at .05 significance level.
with a one-tailed test at .05 significance level.
, now we can calculate the sample size for a given effect size 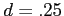 .
As you can see, this is exactly as we did for the dependent samples situation. Just remember that the
.
As you can see, this is exactly as we did for the dependent samples situation. Just remember that the 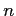 refers to the number of each group.
refers to the number of each group.
An Additional comments on Power
- t tests with evenly distributed participants have greater power than those where the participants are unevenly distributed.
- The dependent samples design has greater power (all else being equal, such as sample size, effect size, etc.) than the independent samples design.
- And, as always, the larger the sample size, the greater the power.
3.5. 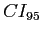
Calculating a Confidence Interval
- Note, we are calculating the interval on the difference between means.
- Recall there are two parts of a confidence interval, the upper limit (UL) and the lower limit (LL).
- The general form of the equations for each limit are:
- In the current situation for the differences between means:
Interpretation of Confidence Interval
- Recall, we had a significance level of .05 (
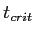 ), so we conducted a 95% confidence interval (
), so we conducted a 95% confidence interval (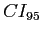 ) on the differences between means.
) on the differences between means.
- The Lower Limit was 1.50 and the Upper Limit was 4.25.
- So, if we drew an infinite number of random samples of viewers of each show, 95% of the differences between means would be between 1.50 and 4.25.
- Remember, the mean of the population of differences between means is fixed (but unknown); while each sample has its own differences between means (samples fluctuate).
3.6. Summary of Section 3
Summary of Section 3
Section 3 covered the following topics:
- The Independent Samples t Test.
- An NHST example of the Independent Samples t Test.
- Cohen's d Effect Size
- Use of delta (
 ) for Statistical Power
) for Statistical Power
- Use of delta (
 ) for calculating a-priori sample size
) for calculating a-priori sample size
- Calculation of Confidence Intervals.



Next: t Summary
Up: Module 8: Introduction to
Previous: Dependent
Contents
jds0282
2010-10-15
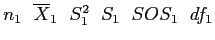
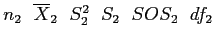
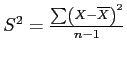 becomes:
becomes:
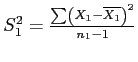 for group 1.
for group 1.
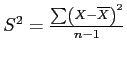 becomes:
becomes:
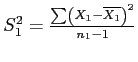 for group 1.
for group 1.
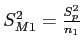
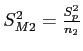
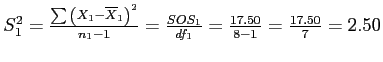
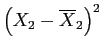
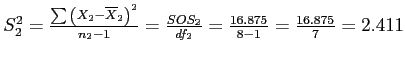
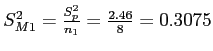
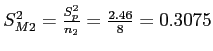
![]() ) for Statistical Power
) for Statistical Power