

Next: M8 Summary
Up: Module 8: Introduction to
Previous: Independent
Contents
4.1. Assumptions
Assumptions for t tests
All statistical analyses have assumptions. If the assumptions are violated, then the analysis is invalidated; meaning, we must either choose a different analysis or modify the existing one in order to have faith in the results.
- Generally speaking, all three t tests have the same assumptions:
- Normality
- Homogeneity of Variance
- Independence
Normality assumption
- The normality assumption refers to the population(s) distribution(s), which are assumed to be normal.
- In the one sample situation, we assume the population distribution is normal.
- In the dependent samples situation, we assume the distribution of differences is normally distributed.
- In the independent samples situation, we assume the distribution of differences between means is normal.
- The t tests can tolerate some deviation from normality, but if skewness and/or kurtosis are greater than
|1.0| in the sample(s) then you should be cautious about proceeding.
Homogeneity of Variances (HOV) assumption
- Does not apply to the one sample t test, but does with the dependent and independent tests.
- This assumption states that each of the two populations (represented by our two sample groups) have equal (homogeneous) variances.
- As the definition implies, the variance of one group should be very similar to the variance of the other group.
- There are empirical tests for this assumption in virtually all statistical software packages.
- If the assumption is violated, there are options available.
- Use trimmed samples; trimming 10 or 20% of the extreme scores (from each group) to make them more homogeneous.
- Use a corrected t test formula, such as t prime (
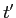 ):
):
Independence assumption
- This assumption refers to the independence of observations (i.e. scores) in the population(s); meaning, each score should not be related to any other score in the group (or sample in the one sample situation).
- Typically, this is handled by random sampling (and random assignment to groups in the case of the independent samples situation).
- If your study did not use random sampling, then you may have a problem with biased results.
- For instance, if you offer compensation for participation (i.e. paying people to be in your study) and an entire community of underprivileged folks show up, then your results are not likely to be applicable to a larger population (i.e. more privileged folks).
4.2. Multiple Test Error Rates
Multiple Tests in one Study
- Family-wise error rate refers to the amount of Type I error (
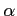 ) associated with multiple tests in one study.
) associated with multiple tests in one study.
- Symbol for a Family-wise error rate of 0.05:
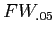
- Family-wise error rate can be controlled by planning for it prior to data collection.
- Say you want to conduct 3 t tests in one study and you want to use an
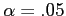 .
.
- Then,
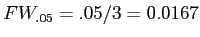
- The 0.0167 is called the pair-wise error rate.
- Each t test is done with
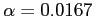 so total error rate is limited to .05 (i.e.
so total error rate is limited to .05 (i.e.
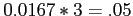 ).
).
- However, such strict significance levels make rejecting the null difficult.
More t Tests
- The discussion above (i.e. Family-wise & Pair-wise error rates) is important for two reasons.
- First, as mentioned on the previous slide, you may want to conduct multiple t tests in one study; as your primary analyses.
- The three types of t tests discussed so far are the primary t tests; meaning, they can be used as the primary analysis of a study.
- However, in future modules you will see there are many more forms of t tests which are used as secondary analyses; meaning, they support a primary analysis.
- In the ANOVA situation t tests can be used for discovering pair-wise differences among multiple groups.
- In the Regression situation t tests are used to evaluate the significance of the weights associated with predictors in a model.
- The bottom line is this, t tests are important and are frequently used; and the issue of cumulative error rates is important.
4.3. Summary of Section 4
Summary of Section 4
Section 4 covered the following topics:
- The Assumptions of t Tests
- Family-wise and Pair-wise Error rates



Next: M8 Summary
Up: Module 8: Introduction to
Previous: Independent
Contents
jds0282
2010-10-15
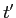 ):
):