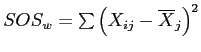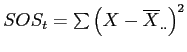


Next: NHST
Up: Module 9: One-Way Analysis
Previous: Contents
Contents
Theoretical Applicability
- The one-way ANOVA is an extension of the Independent Samples t Test.
- Using the one-way ANOVA allows us to analyze more than two groups of one independent variable on one dependent variable.
- The ANOVA family of analysis (all use the F distribution) starts with the one-way situation described just above. However, the general principles and many of the equations are applicable with more than one independent variable.
- In future modules, we will discuss other analysis of the ANOVA family, such as repeated measures and factorial ANOVA, which features more than one independent variable.
Practical Applicability
- 1 IV (with
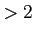 groups) & 1 interval/ratio DV.
groups) & 1 interval/ratio DV.
- The benefit: Can test not only a treatment vs. a control group, but more than one treatment and a control group.
- Some Examples:
- Comparing taste satisfaction ratings of Coke, Pepsi, Mountain Dew, and Dr. Pepper.
- Comparing homophobia scores of persons who are Atheist, Christian, Jewish, or Muslim.
- Comparing the stimulant effects (in terms of alertness) of Cocaine, Crystal Meth., Coffee, Red Bull, Mountain Dew, and Placebo.
Assumptions
- As with the Independent Samples t Test, if our assumptions are not met, we may have difficulty applying our results to the populations of interest or, we may not have any faith in the actual result of the test (i.e. invalid).
- Primary assumptions of one-way ANOVA are exactly as they were for Independent Samples t Test.
- Normality of the population distributions (i.e. each population should be normally distributed).
- Homogeneity of Variance of the population distributions (i.e. each population's variance should be similar).
- Independence of Observations; meaning, each score should be independent of the other scores in its population (i.e. no twins in the same group).
- As with the t test situation, we evaluate these assumptions (of the populations) using the samples as representatives.
A quick note about notation
- Recall from early on, we use subscripts to identify a particular object within a series or collection of objects.
- Here, we will be working extensively with subscripts so it is important to review what the subscripts generally mean.
- On the next few slides you will see a great deal of subscript letters, most are explained on the slide in which they appear first.
- However, recall we use i and j as identifiers of row and column respectively among a table of data (or electronic data file) such that:
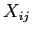
- For example, we have a score:
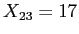 which indicates this score is located at the second row and the third column; or we could say that 17 is the second score of the third variable because, data are generally arranged in a matrix with the variables as column headings and rows representing cases (i.e. participants).
which indicates this score is located at the second row and the third column; or we could say that 17 is the second score of the third variable because, data are generally arranged in a matrix with the variables as column headings and rows representing cases (i.e. participants).
ANOVA
- The statistical procedure for testing variation among the means of more than two groups is called Analysis of Variance (ANOVA).
- NHST with ANOVA is about whether the means of the samples differ more than you would expect if the null hypothesis were true.
- This involves analyzing the variation between the samples (i.e. between the means) and the variation within each sample.
- We analyze the variance to test if there is a significant difference (somewhere) among the means.
- Stated another way, we seek to discover mean differences by analyzing the variances.
- Some authors (textbooks) use `treatment' instead of `between' and `error' instead of 'within'.
Variance
- Recall that conceptually, variance is the sums of squared deviations (
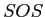 ) divided by the degrees of freedom (
) divided by the degrees of freedom (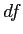 ):
):
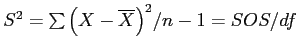
- In ANOVA, we have to calculate the variance for between the groups and the variance within the groups.
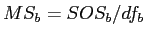
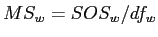
- The ratio of between groups variance to within group variance is our F statistic (
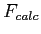 ).
).
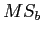
- The between groups variance:
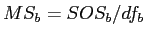
- First, calculate the mean of each group:
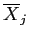
- Then compute the grand mean: Sum of the means, divided by the number of means:
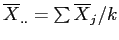 , where
, where 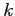 is the number of means (i.e., groups).
is the number of means (i.e., groups).
- Then,
![\(SOS_{b} = \sum{\left[n_{j}\left(\overline{X}_{j} - \overline{X}_{..}\right)^2\right]}\)](img14.png) where
where  is the number of scores in the jth group.
is the number of scores in the jth group.
- The sum of, for each group; the number of scores in the group times the group mean minus the grand mean squared.
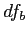 = number of groups minus 1.
= number of groups minus 1.

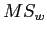
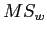 is also called
is also called 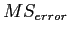 or simply
or simply 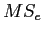
- The within groups variance:
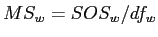
- First, calculate the
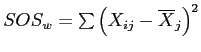
- Then calculate the
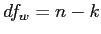
- Then of course;
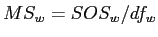
Calculate 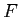
- Simply divide:
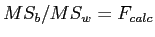
- Use the
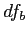 and
and 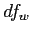 to look up the critical score on the
to look up the critical score on the 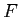 distribution table for the significance level you are using (typically 0.05).
distribution table for the significance level you are using (typically 0.05).
- The `numerator degrees of freedom' is
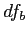 while the `denominator degrees of freedom' is
while the `denominator degrees of freedom' is 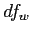
Total 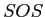 and
and 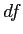
 is the sum of the squared deviations of each individual score around the grand mean.
is the sum of the squared deviations of each individual score around the grand mean.
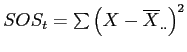
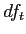 is the total number of scores minus 1.
is the total number of scores minus 1.

- It is not necessary to calculate the totals, but often when hand calculating they are useful for checking previous calculations since;
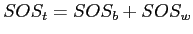 and
and
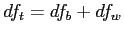
Table 1: Example ANOVA Summary Table
|
Source |
 |
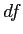 |
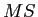 |
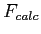 |
|
Between |
64 |
2 |
32 |
11.59 |
|
Within |
58 |
21 |
2.76 |
|
|
Total |
122 |
23 |
|
|
Between and Within should add to Total, if not there was an error in computation.
Recall,  and
and
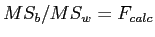
Another way to think about ANOVA
- Previously we said: The ratio of between groups variance to within groups variance is our
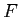 statistic.
statistic.
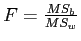
- This could be thought of as: The ratio of differences based on treatment and chance, to the differences based on chance alone, or as the ratio of treatment and error to just error.
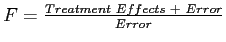
- Simple math principles leave just the treatment effects by `crossing-out' the error terms.
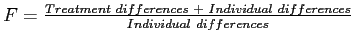
Logic behind NHST One-way ANOVA
- If
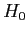 is true, then all the groups will be very similar; their means will be close to one another.
is true, then all the groups will be very similar; their means will be close to one another.
- Between groups variance (
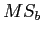 ) will be small.
) will be small.
- If between groups variance is small, then
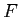 will be small as well; and likely not significant (
will be small as well; and likely not significant (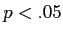 ).
).
- If
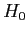 is not true, then all the groups will be very different.
is not true, then all the groups will be very different.
- Between groups variance and
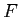 will be larger; and likely significant (
will be larger; and likely significant (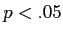 ).
).
- Conversely; if within groups variance is small, then
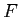 will be large and if within groups variance is large,
will be large and if within groups variance is large, 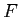 will be small.
will be small.
- Remember;

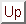


Next: NHST
Up: Module 9: One-Way Analysis
Previous: Contents
Contents
jds0282
2010-10-21
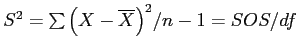
![\(SOS_{b} = \sum{\left[n_{j}\left(\overline{X}_{j} - \overline{X}_{..}\right)^2\right]}\)](img14.png) where
where