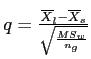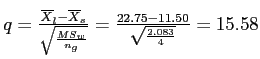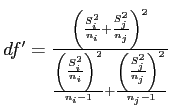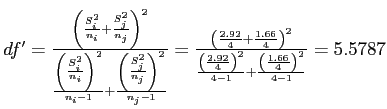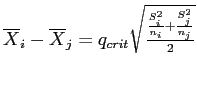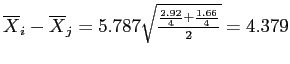


Next: Effect Size
Up: NHST
Previous: Comparisons
Contents
Post-hoc Testing
- In exploratory research, you would test all possible combinations of groups to determine where the significant differences are located (typically only if the omnibus
 is significant).
is significant).
- Most researchers always do either planned comparisons (preferred) or post-hoc testing (exploratory), because the omnibus
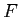 is not terribly informative on its own.
is not terribly informative on its own.
- There are many types of post-hoc procedures, each has strengths and weaknesses ... but, some are better than others.
- Some suggestions:
- If assumptions met: Tukey's HSD or REGW-Q.
- If unequal group sizes: Games-Howell.
- If unequal variances: Games-Howell.
More on Post-hoc tests in general
- Most post-hoc tests rely on the
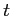 distribution or a modification of it.
distribution or a modification of it.
- FYI:
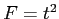 which means, the simple (two group) comparisons above can be converted with
which means, the simple (two group) comparisons above can be converted with 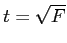
- The modified
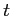 distribution is often called the Studentized t statistic.
distribution is often called the Studentized t statistic.
- Symbol for the Studentized
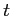 is:
is: 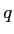
- It is defined by:
- where
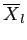 refers to the largest mean among the groups,
refers to the largest mean among the groups,
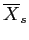 the smallest, and
the smallest, and 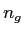 is the number of individuals per group.
is the number of individuals per group.
More on 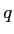
- When using
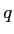 we first must rank the means from smallest to largest.
we first must rank the means from smallest to largest.
- For our example:
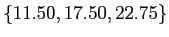
- There are 3 means in this set,
 which is used in looking up values in the
which is used in looking up values in the 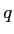 table (the table below uses the familar
table (the table below uses the familar 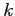 instead of
instead of 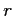 but, most use
but, most use 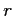 ).
).
- Using the formula from above, we can solve for
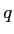
- So
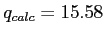 and we can use
and we can use  , significance level of 0.05, and
, significance level of 0.05, and 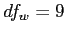 to find
to find
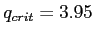 in the
in the  table.
table.
- Given
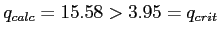 , we reject the null hypothesis and conclude there was a significant difference between the largest and smallest means.
, we reject the null hypothesis and conclude there was a significant difference between the largest and smallest means.
- Which can replace the omnibus
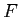 , but with less statistical power.
, but with less statistical power.
Tukey's Honestly Significant Differences test
- Tukey's HSD is considered one of the original post-hoc tests and offers a fixed family-wise error rate at alpha (significance level).
- Once we have ranked the means
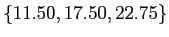 and found our critical value (
and found our critical value (
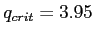 ) we can calculate the minimum difference between means needed to discover a significant difference.
) we can calculate the minimum difference between means needed to discover a significant difference.
- So, if a mean difference (
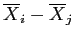 ) is larger than 2.85 we would conclude there is a significant difference between those two means.
) is larger than 2.85 we would conclude there is a significant difference between those two means.
Tukey's HSD continued
- With our minimum significant difference calculated at 2.85; we can compare the differences among our three means to it, to determine which means differ significantly from the others.
|
Green |
Blue |
Red |
 |
11.50 |
17.50 |
22.75 |
|
Green = 11.50 |
0 |
6.00 |
11.25 |
|
Blue = 17.50 |
- |
0 |
5.25 |
|
Red = 22.75 |
- |
- |
0 |
- So, we find a significant difference between each pair of means because, each difference is greater than 2.85.
Games-Howell Post-hoc Test
- The Tukey test above assumes equal sample sizes for each group and equal variances among the groups.
- Often `real data' do not conform to what we would expect and these assumptions are often violated.
- The Games-Howell test provides a method for when either (or both) of the assumptions are not upheld.
- Essentially, this test incorporates the samples sizes and variances of each group being compared.
- The
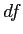 and the critical difference between means (
and the critical difference between means (
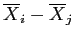 ) are modified for inclusion of samples sizes and variances.
) are modified for inclusion of samples sizes and variances.
Games-Howell modification of 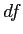
- Until now we have consistently used
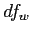 for finding our critical values (e.g.,
for finding our critical values (e.g., 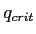 ).
).
- With the Games-Howell test, we actually calculate
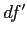 using each groups' sample size and variance; such that for each pair of groups:
using each groups' sample size and variance; such that for each pair of groups:
- where subscript
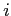 and subscript
and subscript 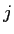 identify descriptive statistics from each group being compared.
identify descriptive statistics from each group being compared.
Example 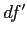
As an example let's consider the Red and Green groups.
- Red (i):
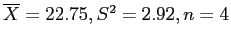
- Green (j):
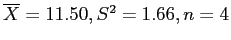
- Pay careful attention to the fact that
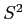 is a symbol, not an operation.
is a symbol, not an operation.
- See the supplemental handout for an example of the complete, step-by-step calculation.
Games-Howell difference between means
Minimum Significant Difference
- So, given
 , significance level of 0.05, and now
, significance level of 0.05, and now 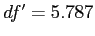 we look to the
we look to the  table and find:
table and find:
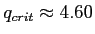
- Where earlier we had:
- Now, for each pair of means, we have:
- For the current Red vs. Green example:
Red
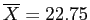 and Green
and Green
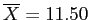
- Given our minimum significant difference (for this pair) of 4.379, we need an actual mean difference larger than this to conclude a significant difference was present.
- Clearly,
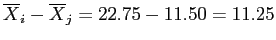 is greater than 4.379; which indicates the Red group recalled significantly more words than the Green group.
is greater than 4.379; which indicates the Red group recalled significantly more words than the Green group.
- Just remember, all that calculating must be done for each group because each group may have a different sample size and more than likely will have a different variance (
 ).
).
- The ANOVA and associated tests of individual means (planned comparisons or post-hoc tests) are vulnerable to violations of the homogeneity assumption.
- Therefore, the Games-Howell test is highly recommended.



Next: Effect Size
Up: NHST
Previous: Comparisons
Contents
jds0282
2010-10-21
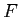 is not terribly informative on its own.
is not terribly informative on its own.