CI

Next: Graphs Up: NHST Previous: Effect Size Contents

Confidence Intervals

In the ANOVA situation, Confidence Intervals (CIs) are not meaningful, until you get down to testing individual pairs of means.

At the level of planned comparisons or post-hoc testing, CIs are meaningful.
In the situation of testing individual pairs of means, we could review the previous module ( 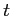$t$ tests) and apply those methods to the current testing of individual pairs of means - for calculating a CI (and Cohen's $d$ ).
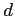Or, we could use current information and our general understanding of the equations for the upper limit (UL) and lower limit (LL) of a CI.
- Recall the general equations for CI limits:

$UL = \left(+crit\right)*\left(SE\right) + mean$
$LL = \left(-crit\right)*\left(SE\right) + mean$

CI for Planned Comparisons

During planned comparison testing, we were interested in the difference between pairs of group means and we had all the elements we needed to compute the UL and LL for each comparison.

Here we apply those elements to the general form of the UL and LL equations for each Planned Comparison.
- However, we are now in a two group comparison (essentially 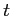$t$ testing) so given that 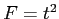$F = t^2$ we need to take the square root of $F_{crit}$ and $MS_{w}$ .

$UL = \sqrt{\left(+F_{crit}\right)*\left(MS_{w}\right)} + \overline{X}_{i} - \overline{X}_{j}$
$LL = \sqrt{\left(-F_{crit}\right)*\left(MS_{w}\right)} + \overline{X}_{i} - \overline{X}_{j}$

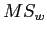Adjustments for square root of a negative

As many of you know, you can not take the square root of a negative number.
So, recognize that the formulas below are equivalent for what we want to do above.

$UL = \sqrt{\left(F_{crit}\right)*\left(MS_{w}\right)} + \overline{X}_{i} - \overline{X}_{j}$
$LL = \sqrt{\left(F_{crit}\right)*\left(MS_{w}\right)} - \overline{X}_{i} - \overline{X}_{j}$

CI for Example Planned Comparisons (PC)

CI for PC 1: Red ( 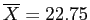$\overline{X} = 22.75$ ) vs. Blue ( $\overline{X} = 17.50$ )

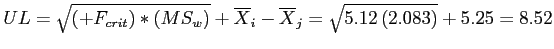
$UL = \sqrt{\left(+F_{crit}\right)*\left(MS_{w}\right)} + \overline{X}_{i} - \overline{X}_{j} = \sqrt{5.12\left(2.083\right)} + 5.25 = 8.52$
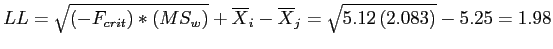
$LL = \sqrt{\left(-F_{crit}\right)*\left(MS_{w}\right)} + \overline{X}_{i} - \overline{X}_{j} = \sqrt{5.12\left(2.083\right)} - 5.25 = 1.98$

If we drew an infinite number of samples, we would expect 95% of the mean differences between the Red and Blue groups to be between 8.52 and 1.98.

CI for PC 2: Green ( 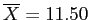$\overline{X} = 11.50$ ) vs. Blue ( $\overline{X} = 17.50$ )

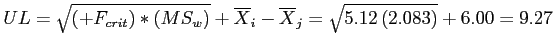
$UL = \sqrt{\left(+F_{crit}\right)*\left(MS_{w}\right)} + \overline{X}_{i} - \overline{X}_{j} = \sqrt{5.12\left(2.083\right)} + 6.00 = 9.27$
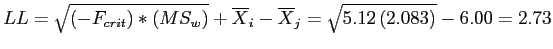
$LL = \sqrt{\left(-F_{crit}\right)*\left(MS_{w}\right)} + \overline{X}_{i} - \overline{X}_{j} = \sqrt{5.12\left(2.083\right)} - 6.00 = 2.73$

If we drew an infinite number of samples, we would expect 95% of the mean differences between the Green and Blue groups to be between 9.27 and 2.73.

CI for Tukey's HSD Post-hoc (PH) test

With Tukey's Post-hoc testing, we are using modified 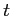$t$ tests, so we can simply use the calculated minimum difference between means (2.85) from earlier.

CI for PH 1: Red ( 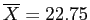$\overline{X} = 22.75$ ) vs. Blue ( $\overline{X} = 17.50$ )

$UL = \left(+q_{r=3,.05}\right) + \overline{X}_{i} - \overline{X}_{j} = +2.85 + 5.25 = 8.10$
$LL = \left(-q_{r=3,.05}\right) + \overline{X}_{i} - \overline{X}_{j} = -2.85 + 5.25 = 2.40$

If we drew an infinite number of samples, we would expect 95% of the mean differences between the Red and Blue groups to be between 8.10 and 2.40.
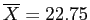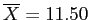CI for PH 2: Red ( $\overline{X} = 22.75$ ) vs. Green ( $\overline{X} = 11.50$ )

$UL = \left(+q_{r=3,.05}\right) + \overline{X}_{i} - \overline{X}_{j} = +2.85 + 11.25 = 14.10$
$LL = \left(-q_{r=3,.05}\right) + \overline{X}_{i} - \overline{X}_{j} = -2.85 + 11.25 = 8.40$

If we drew an infinite number of samples, we would expect 95% of the mean differences between the Red and Green groups to be between 14.10 and 8.40.
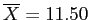CI for PH 3: Blue ( $\overline{X} = 17.50$ ) vs. Green ( $\overline{X} = 11.50$ )

$UL = \left(+q_{r=3,.05}\right) + \overline{X}_{i} - \overline{X}_{j} = +2.85 + 6.00 = 8.85$
$LL = \left(-q_{r=3,.05}\right) + \overline{X}_{i} - \overline{X}_{j} = -2.85 + 6.00 = 3.15$

If we drew an infinite number of samples, we would expect 95% of the mean differences between the Green and Blue groups to be between 8.85 and 3.15.

Next: Graphs Up: NHST Previous: Effect Size Contents

jds0282 2010-10-21