MODULE 8

Continuation of the previous tutorial notes regarding SEM.

XIII. Structural Equation Modeling (SEM) using PROC CALIS

First, let's take a moment to review our fictional* model. Our model consists of 13 manifest variables which are assumed to measure four latent factors. The first latent factor, Personality, is assumed to be measured by Extroversion (extro), Openness (open), and Agreeableness (agree). The second latent factor, Engagement, is assumed to be measured by Social Engagement (social), Cognitive Engagement (cognitive), Physical Engagement (physical), and Cultural Engagement (cultural). The third latent factor, Crystallized Intelligence, is assumed to be measured by the established tests of Vocabulary (vocab), Abstruse Analogies (abstruse), and Block Design (block). The fourth latent factor, Fluid Intelligence, is assumed to be measured by the established tests of Common Analogies (common), Letter Sets (sets), and Letter Series (series). The general research question for our fictional longitudinal study concerns whether or not certain personality traits cause persons to lead an engaged lifestyle, and do these personality traits and leading an engaged lifestyle prevent loss of cognitive functioning in late life (e.g. beyond 65 years of age).

*Again; this is a fictional example; it includes simulated data and is not meant to be taken seriously as a research finding supported by empirical evidence. It is merely used here for instructional example purposes.

If you are unfamiliar with standard path and structural equation models; there are a few things you should take note of in our diagram that tend to be seen in published materials displaying path models and structural equation models. First, the use of squares or rectangles to denote observed or measured variables (often referred to as manifest variables or indicator variables). Second, the use of circles or ellipses to denote unobserved or latent variables (often referred to as latent factors). Third, the use of straight, single headed arrows to denote causal relationships. There are two types of causal relationships shown in most diagrams. The assumed causal relationship between a latent factor and its indicator or manifest variables which are often referred to as loadings or factor loadings or factor coefficients. The hypothesized causal relationship between two latent factors which are often referred to as paths or path loadings or path coefficients. And fourth, the use of curved, double-headed arrows to refer to bi-directional relationships (often referred to as correlations or covariances). Specific hypotheses should be used to clarify what the researcher expects to find (e.g. a positive bi-directional relationship or correlation between Crystallized & Fluid Intelligences).

From this point forward, we will use the term loading to refer to a relationship between a manifest variable and a latent factor. We will use the term path to refer to the relationship between two latent factors.

Something to consider when conducting SEM is the recommendation of using a two stage process to conduct the SEM (Anderson & Gerbing, 1988). When using two stages, the first stage is used to verify the measurement model. Verification of the measurement model in SEM can be considered analogous to conducting a confirmatory factor analysis. The purpose is to ensure you are measuring (adequately) what you believe you are measuring. Essentially, you are verifying the factor structure. When verifying the measurement model, you are more concerned with the error variances and the loadings than with the relationships between latent factors (paths). Recall, the loadings are those which represent the relationships between a factor and its manifest indicator variables. The second stage involves actually testing the hypothesized causal relationships between factors, also referred to as testing the structural model, which is where you are interested more in the paths than the loadings. Recall, the paths represent the hypothesized causal relationships between latent factors.

# Anderson, J. C., & Gerbing, D. W. (1988). Structural equation modeling in
#      practice: A review and recommended two-step approach. Psychological
#      Bulletin, 103, 411 - 423.

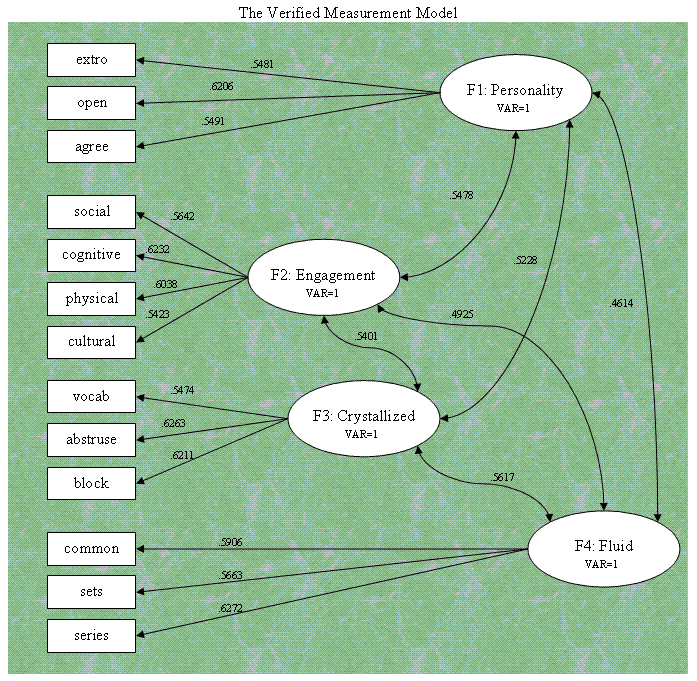
Below you will see the verified Measurement Model from the previous tutorial Stage 1.

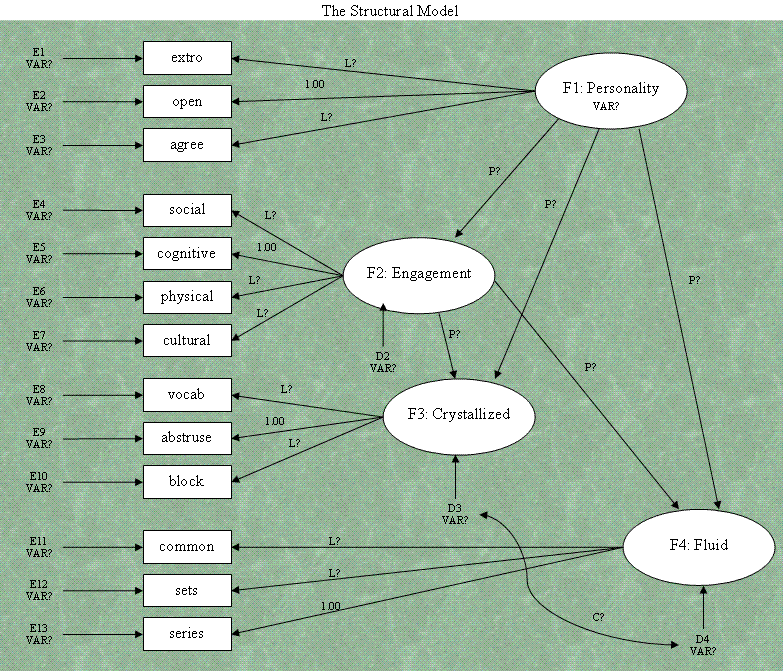
Stage II: Testing the Structural model.

Below you'll find a diagram which represents our structural model. Notice we are now concerned with the relationships between latent factors, those paths will be estimated. Also notice, the variances of the factors are no longer fixed at 1. This time, we must fix the largest one of loadings from each of the factors to 1 in order to set the scale of the factors and estimate their variances (and disturbance terms). Disturbance terms (D2, D3, D4) are new here and represent the error associated with each factor which can be thought of as any causal influence for that factor which was not included in the model. Also notice there is no disturbance term specified for our one exogenous factor. Disturbance terms are only specified for endogenous factors.

One of the key requirements of Path Analysis and SEM is overidentification. A model is said to be overidentified if it contains more unique inputs (sometimes called informations) than the number of parameters being estimated. In our example, we have 13 manifest variables. We can apply the following formula to calculate the number of unique inputs:

(1)                                                  number of unique inputs = (p ( p + 1 ) ) / 2

where p = the number of manifest variables. Given this formula and our 13 manifest variables; we calculate 91 unique inputs or informations which is greater than the number of parameters we are estimating. Looking at the diagram, we see 1 covariance (C?), 9 loadings (L?), 5 paths (P?), 3 disturbance terms (VAR?), 1 factor variance (VAR?) and 13 error variances (VAR?). Adding these up, we get 32 parameters to be estimated. You'll notice, as discussed above, that for our structural model, we have fixed the largest loading for each latent factor to be 1 (L = 1). This is done to allow estimation of the disturbance terms and the first factor's variance. Also notice that we can no longer estimate the correlation/covariance between F3 and F4 (as was done when verifying the measurement model), instead we estimate the correlation (C?) between the disturbance terms of those two endogenous factors. Remember too that SEM requires large sample sizes. Several general rules have been put forth as lowest reasonable sample size estimates; at least 200 cases at a minimum, at least 5 cases per manifest or measured variable, at least 400 cases, at least 25 cases per measured variable, 5 observations or cases per parameter to be estimated, 10 observations or cases per parameter to be estimated...etc. The bottom line is this; SEM is powerful when done with adequately large samples --  the larger the better. Another issue related to sample size, is the recommendation of having at least 3 manifest variables for each latent factor (Anderson & Gerbing, 1988). Another consideration is that of remaining realistic when setting out to study a particular phenomena with SEM in mind as the analysis. It is often easy to develop some very sophisticated models containing a great number of manifest and latent variables. However, complex models containing more than 20 manifest variables can lead to confusion in interpretation and a lack of fit, as well as convergence difficulty. Bentler and Chou (1987) recommend a limit of 20 manifest variables.

# Bentler, P. M., & Chou, C. (1987). Practical issues in structural modeling. Sociological  
#      Methods & Research, 16, 78 - 117.

The procedure for conducting SEM in SAS is PROC CALIS; however, PROC CALIS needs to have the data fed to it. Here we will use the correlation matrix with number of observations and standard deviations as was done previously.

Using the the same values from the previous tutorial (number of observations, standard deviations, & correlation matrix) when verifying the Measurement Model; we can proceed to the Structural Model. The syntax for testing our Structural Model is displayed below. Note that the top half of the syntax simply enters the data and is identical to what was used in verifying the Measurement Model. The second half (beginning with PROC CALIS) is substantively different from that used in verifying the Measurement Model; and this new syntax is used to test the Structural Model. Notice we have left out the option for requesting the modification indices. 

DATA sem1(TYPE=CORR);
INPUT _TYPE_ $ _NAME_ $ V1-V13;
LABEL
V1 = 'extro'
V2 = 'open'
V3 = 'agree'
V4 = 'social'
V5 = 'cognitive'
V6 = 'physical'
V7 = 'cultural'
V8 = 'vocab'
V9 = 'abstruse'
V10 = 'block'
V11 = 'common'
V12 = 'sets'
V13 = 'series'
;
CARDS;
N . 750 750 750 750 750 750 750 750 750 750 750 750 750
STD . 9.0000 6.0000 5.2500 15.0000 7.5000 3.7500 11.2500 8.2500 3.0000 3.0000 6.7500 12.0000 7.5000
CORR V1 1.0000 . . . . . . . . . . . .
CORR V2 .3385 1.0000 . . . . . . . . . . .
CORR V3 .3056 .3388 1.0000 . . . . . . . . . .
CORR V4 .1196 .1842 .2111 1.0000 . . . . . . . . .
CORR V5 .1889 .1970 .1691 .3685 1.0000 . . . . . . . .
CORR V6 .1475 .2099 .1926 .3234 .4054 1.0000 . . . . . . .
CORR V7 .1932 .2264 .1664 .3044 .3044 .3254 1.0000 . . . . . .
CORR V8 .1070 .1755 .1349 .1967 .1843 .1495 .1951 1.0000 . . . . .
CORR V9 .1563 .2082 .1724 .2056 .1290 .1905 .1971 .3659 1.0000 . . . .
CORR V10 .2076 .2207 .2062 .2196 .2012 .2116 .2223 .3383 .3725 1.0000 . . .
CORR V11 .1900 .1784 .1298 .1168 .1816 .1581 .1841 .1483 .1996 .1932 1.0000 . .
CORR V12 .1443 .1288 .0980 .1573 .2387 .2020 .1554 .1452 .2484 .1819 .3399 1.0000 .
CORR V13 .2136 .1707 .1571 .1589 .1821 .1364 .1940 .1752 .2522 .2316 .3765 .3437 1.0000
;

PROC CALIS COVARIANCE CORR RESIDUAL;
LINEQS
V1 = LV1F1 F1 + E1,
V2 = F1 + E2,
V3 = LV3F1 F1 + E3,
V4 = LV4F2 F2 + E4,
V5 = F2 + E5,
V6 = LV6F2 F2 + E6,
V7 = LV7F2 F2 + E7,
V8 = LV8F3 F3 + E8,
V9 = F3 + E9,
V10 = LV10F3 F3 + E10,
V11 = LV11F4 F4 + E11,
V12 = LV12F4 F4 + E12,
V13 = F4 + E13,
F2 = PF2F1 F1 + D2,
F3 = PF3F1 F1 + PF3F2 F2 + D3,
F4 = PF4F1 F1 + PF4F2 F2 + D4;
STD
F1 = VARF1,
D2 = VARD2,
D3 = VARD3,
D4 = VARD4,
E1-E13 = VARE1-VARE13;
COV
D3 D4 = CD3D4;
VAR V1-V13;
RUN;

The PROC CALIS statement is followed by options. First, COVARIANCE tells SAS we want to use the covariance matrix to perform the analysis. Even though we are using the correlation matrix as our data input, SAS calculates the covariance matrix for the PROC CALIS. That is why the number of observations and standard deviations must be included with the correlations. The CORR option specifies that we want the output to include the correlation matrix or covariance matrix on which the analysis is run. The RESIDUAL option allows us to see the absolute and standardized residuals in the output. The next part of the syntax, LINEQS, provides SAS with the specific linear equations which specify the loadings and paths we want estimated. The first of which can be read as: variable 1 equals factor 1 and the error variance associated with variable 1. In the second lineqs line; you'll see how we have fixed the loading of V1 to F1 at 1.00. When a path or loading is left our, CALIS fixes it as 1.00. Also notice the last lineqs statement which can be read as factor 4 equals the estimated path between factor 4 and factor 1 plus the estimated path between factor 4 and factor 2, and the error (disturbance term) associated with factor 4. Next, we see the STD lines which specify which variances we want estimated. The variance of our only exogenous factor (factor 1) is listed as VARF1. The variable error variances are being estimated as VARE1 through VARE13 and the disturbance terms are listed as VARD2 through VARD4. Last, the COV statements specify all the covariances which need to be estimated; here there is only one, which reflects the correlation between the disturbance terms for factor 3 and factor 4. Then, the VAR line simply lists the variables to be used in the analysis; V1 through V13. When creating syntax on your own; be very careful and attentive as to where semi colons are placed.

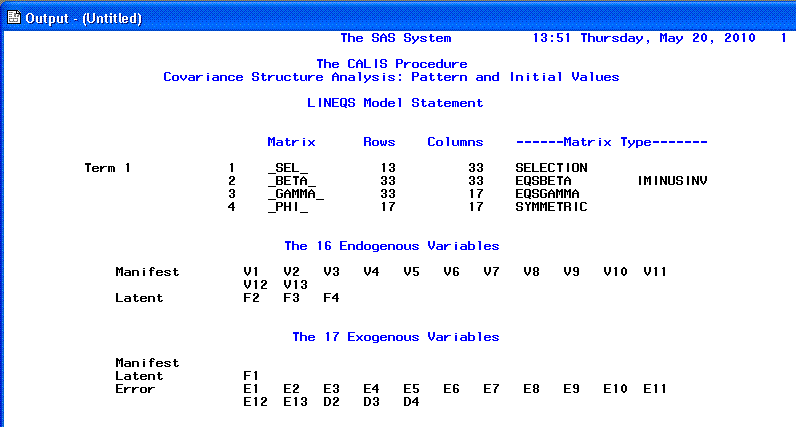
The first page of the PROC CALIS output (below) consists of general information, including the number of endogenous variables (any variable with a straight single-headed arrow pointing at it) and the number of exogenous variables (any variable without any straight single-headed arrows pointing to it).

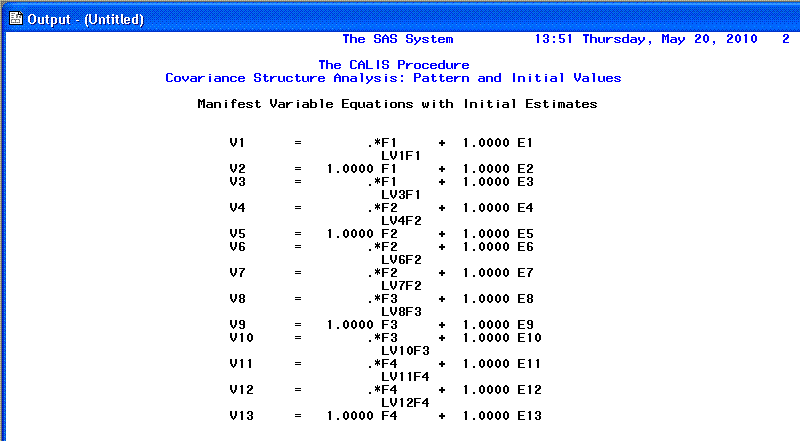
The second page of the PROC CALIS output consist of a listing of the loading parameters to be estimated (those associated with our manifest variables); essentially a review of the top part of specified model from the CALIS syntax. Again; we can see that each factor has one loading fixed at 1.00.

The third page of the output contains a listing of the latent variable parameters to be estimated, the variances, and the covariances to be estimated.

The fourth page and fifth pages show the general components of the model (e.g. number of variables, number of informations, number of parameters, etc.); as well as the descriptive statistics and covariance matrix for the variables entered in the model. The covariance matrix starts on the fourth page and continues onto the fifth page.

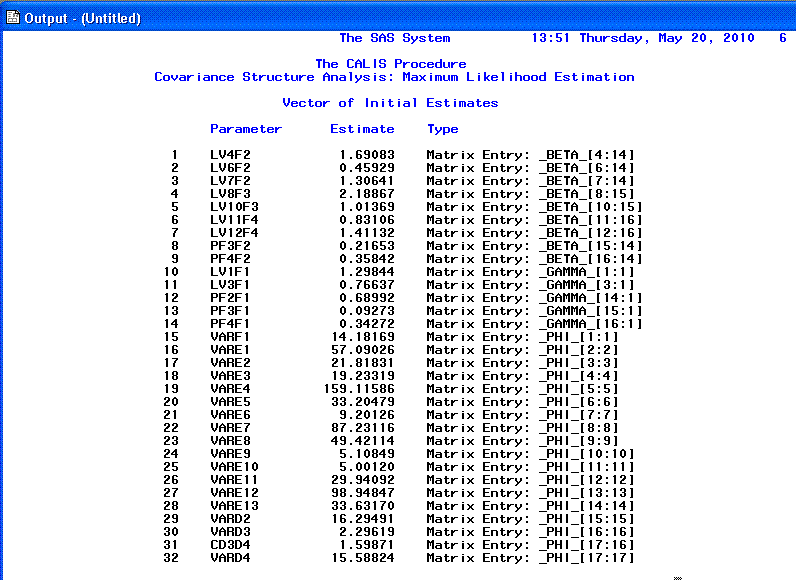
The 6th page provides the initial parameter estimates.

The 7th page includes the iteration history. Often it is important to focus on the last line of the Optimization results (left side of the bottom of the page) which states whether or not convergence criterion was satisfied.

The 8th and 9th pages contain the predicted covariance matrix, which is used for comparison to the matrix of association (original covariance matrix) to produce residual values.

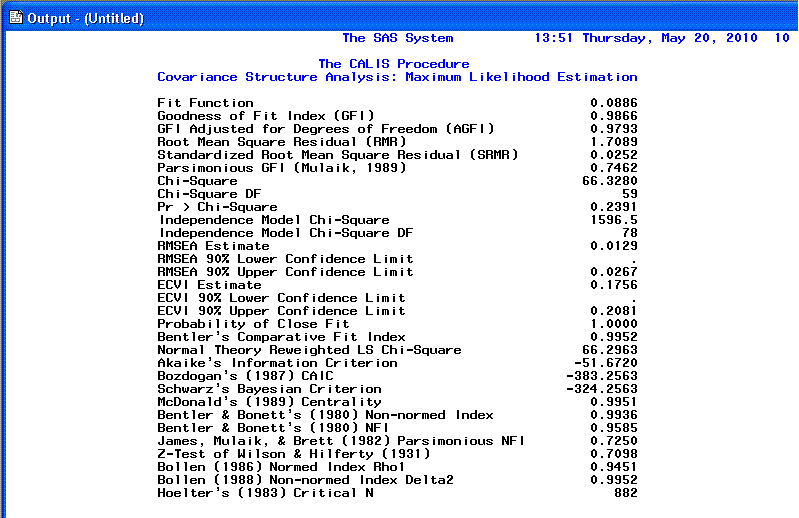
The 10th page displays fit indices. As you can see, a fairly comprehensive list is provided. Please note that although Chi-square is displayed it should not be used as an interpretation of goodness-of-fit due to the large sample sizes necessary for SEM (which inflates the chi-square statistic to the point of meaninglessness). Some of the more commonly reported fit indices are the RMSEA (root mean square error of approximation), which when below .05 indicates good fit; the Schwarz's Bayesian Criterion (also called BIC; Bayesian Information Criteria), where the smaller the value (i.e. below zero) the better the fit; and the Bentler & Bonnett's Non-normed Index (NNFI) as well as the Bentler & Bonnett's normed fit index (NFI)--both of which should be greater than .90 and above to indicate good fit. 

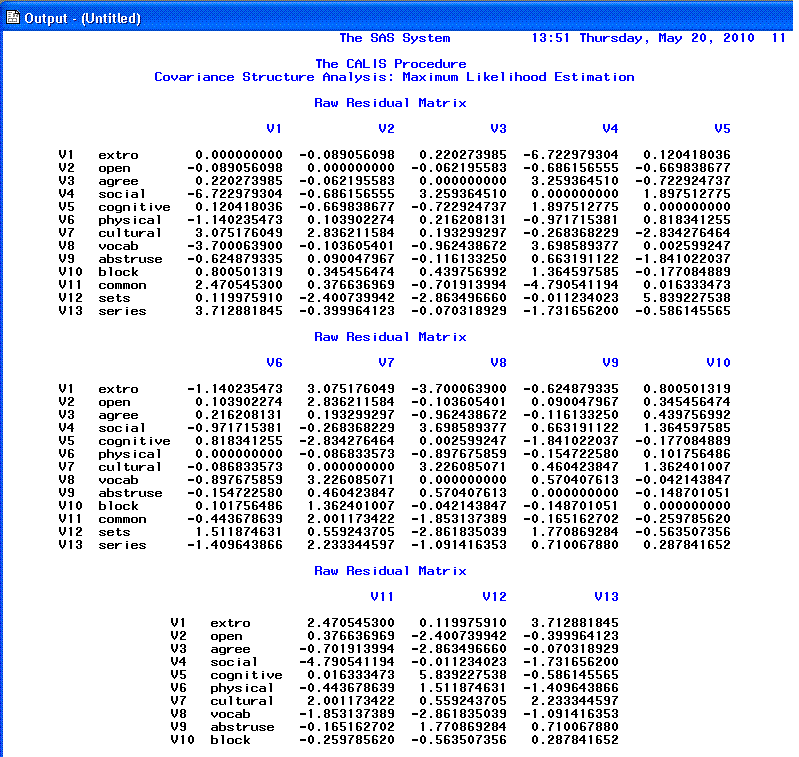
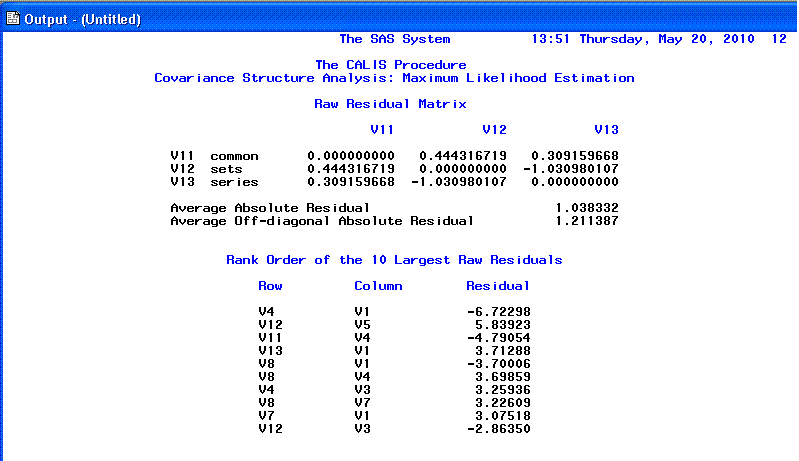
Page 11 and 12 provide the Raw residual matrix and the ranking of the 10 largest Raw residuals.

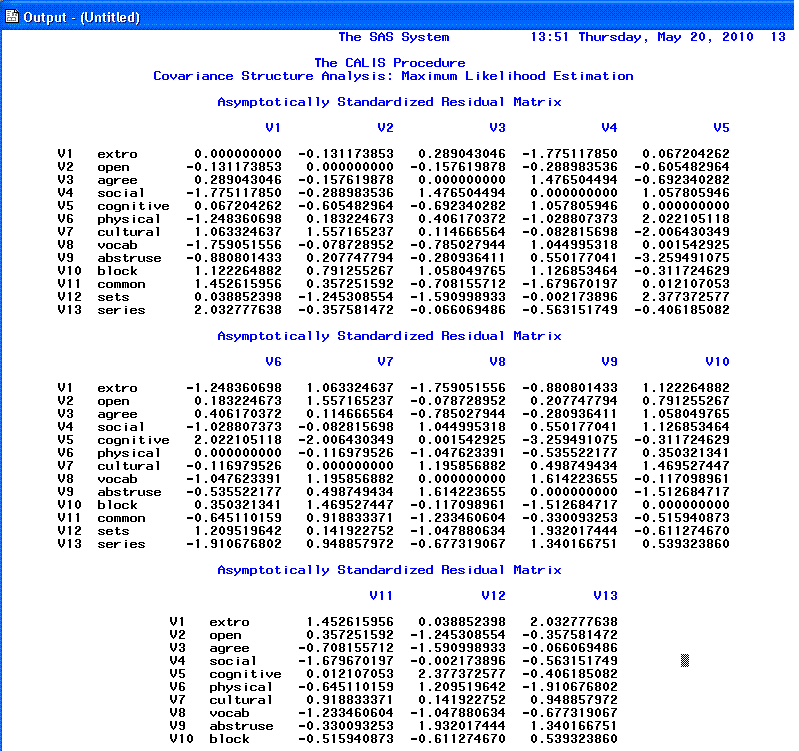
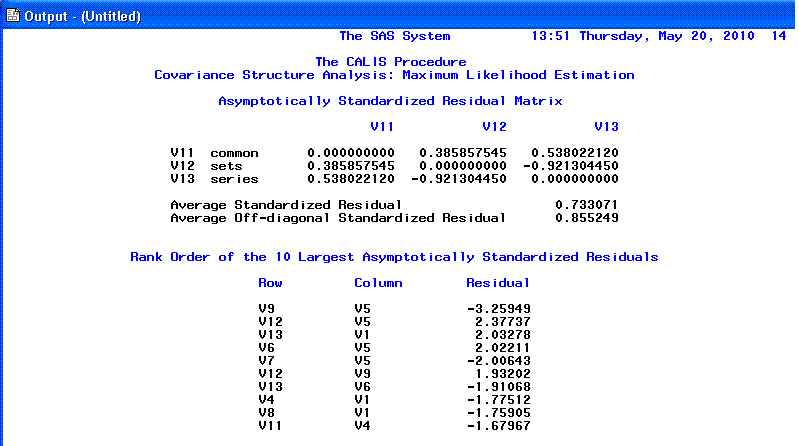
The 13th and 14th pages show the Standardized residual matrix and the 10 largest Standardized residuals; we expect values close to zero which indicates good fit. Any values greater than |2.00| indicates lack of fit and should be investigated. This is really the heart of evaluating goodness of fit; if fit is truly good, you would see virtually no difference between the original covariance matrix and the predicted covariance matrix (i.e. each of the residuals would be zero). Here in this example, we have a few values greater than |2.00| which is a bit worrisome.

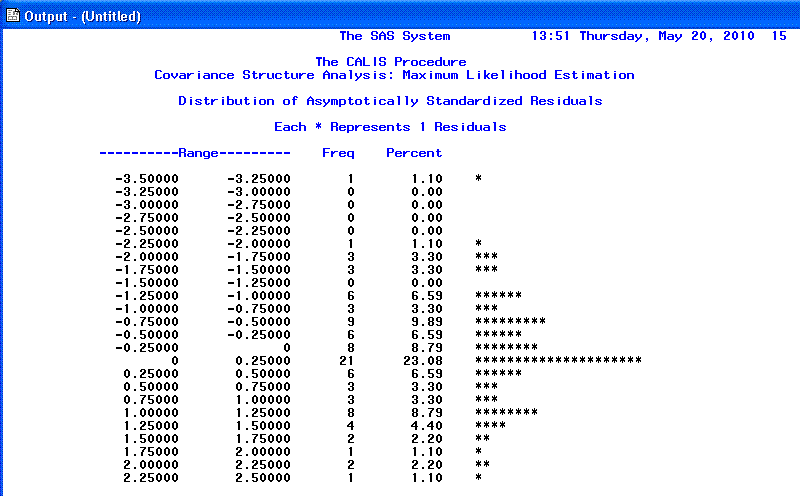
The 15th page displays a sideways histogram of the distribution of the Standardized residuals. Generally we expect to see a normal distribution of residuals with no values greater than |2.00|. Here we see a couple of values in each tail of the distribution of residuals which are slightly larger than we would like to see.

The 16th page displays our loadings (coefficients) in Raw form, as well as t-values and standard errors for the t-values associated with each. Remember that t-values for coefficients (here loadings) are statistically significant (p < .05, two-tailed) if their absolute value is greater than 1.96; meaning they are significantly different from zero. If the t-value is greater than 2.58, then p < .01 and if the t-value is greater than 3.29, then p < .001. It is also recommended that a review of the standard errors be performed, as extremely small standard errors (those very close to zero) may indicate a problem with fit associated with one variable being linearly dependent upon one or more other variables. Here, all our t-values for our factor loadings are greater than 3.29 and none of our standard errors are noticeably low (i.e. less than .0099 for instance). We also notice the four loadings we fixed at 1.000 (V2, V5, V9, & V13).

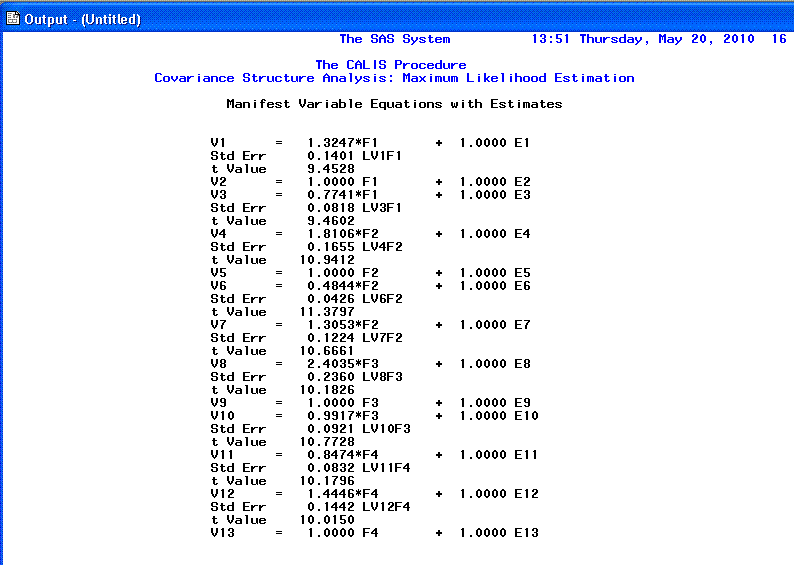
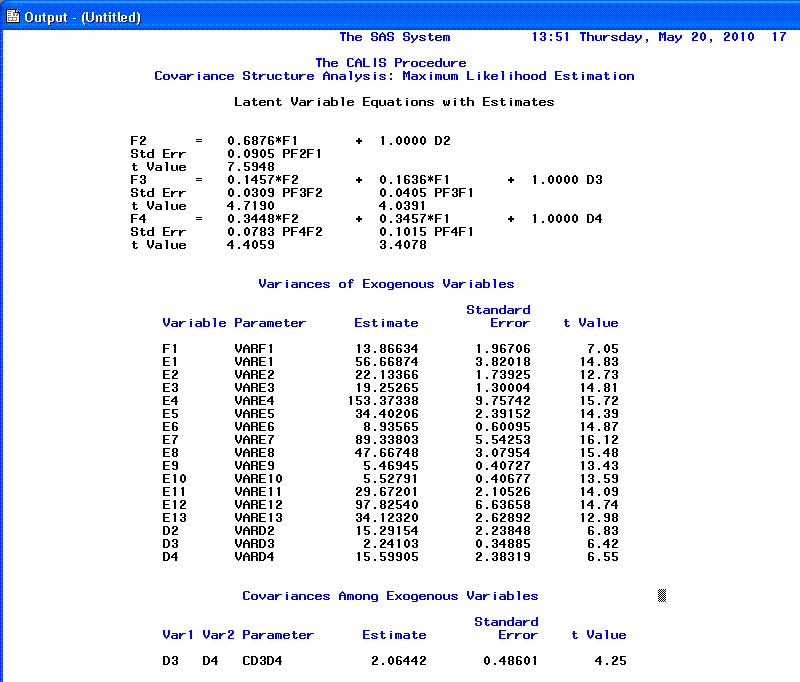
On the 17th page, we see estimated paths in raw scale, estimated variance parameters and the estimated covariance between our F3 and F4 disturbance terms; each with t-values and standard errors for the t-values. All of our t-values were greater than 3.29 and therefore, significantly different from zero (p < .001). Notice at the top the variance estimates we find F1 as asked for in the syntax. This was the only factor we estimated variance for because, it was our only exogenous factor.

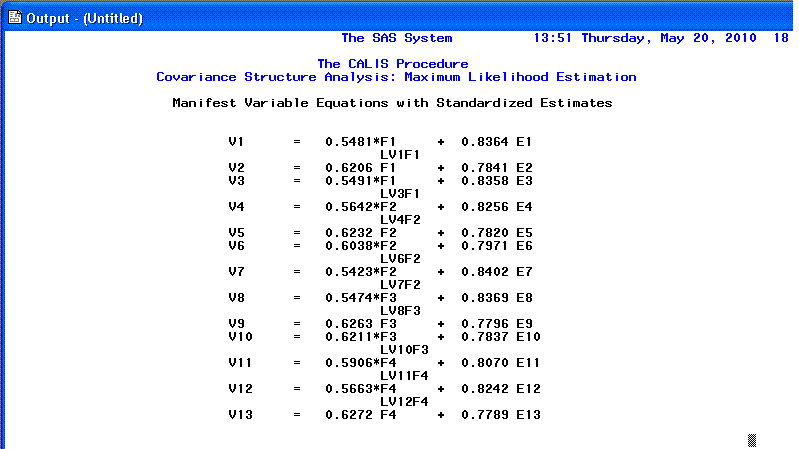
The 18th page provides Standardized factor loadings (coefficients; analogous to β). These are what get reported both in text descriptions and in figures/diagrams. You will also notice they are identical to what we found in our verification of the Measurement Model in the previous tutorial. 

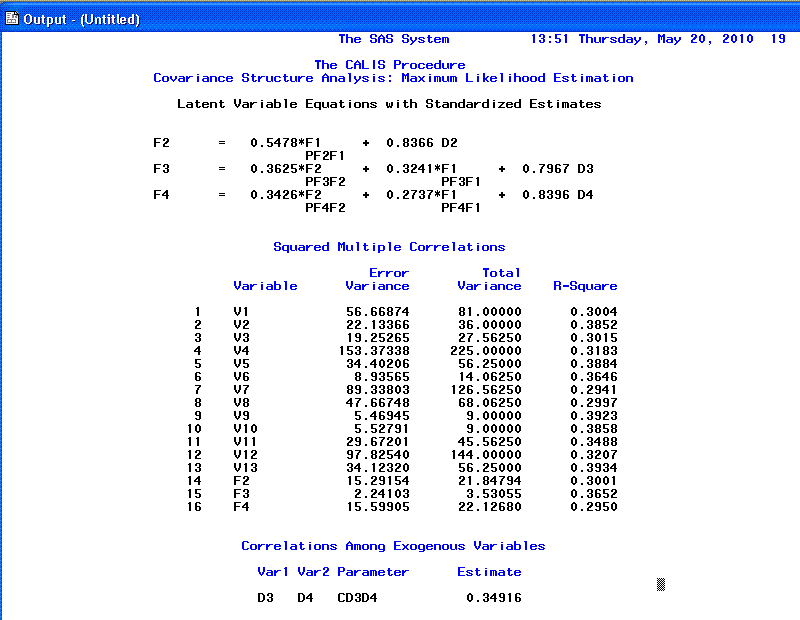
The 19th page displays our standardized path estimates (also analogous to β and reported in text descriptions and diagrams) and the 'Squared Multiple Correlations'. The R-square column gives us an idea of how well our manifest variables reflect the latent factors because, these values are interpreted as the percentage of variance accounted for in our manifest variables by their respective factors. As an example; we could interpret V1 (Extroversion) as having 30.004% of its variance accounted for by F1 (Personality). You'll notice, the R? value is simply the square of the standardized loading (e.g. .5481? = .3004). Furthermore, if we square our E1 term (.8364; previous page), we get .6996, which when added to the variance accounted for by the factor (.3004) gives us the complete standardized variance of our V1 variable: 1.00. This confirms our classical test theory perspective of observed score = true score (the amount of the latent factor) + error.

If we had asked for modification indices, the 20th page would begin displaying them. However we did not specify them here because, as discussed previously they are based on chi-square and chi-square does not provide an honest measure of goodness-of-fit.

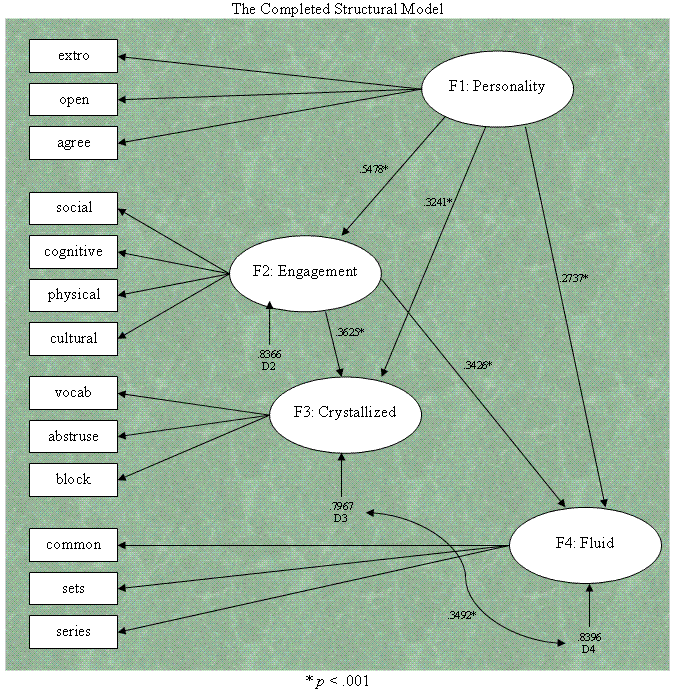
Below you will find our completed Structural Model diagram with standardized path coefficients. Notice, the disturbance terms do not get flagged, even though we did have t-values for them.

This concludes the tutorial on Structural Equation Modeling.

Please realize, this tutorial is not an exhaustive review, merely an introduction. It is not meant to be a replacement for one or several good textbooks.

Return to the SAS Short Course