MODULE 9

The SPSS CATREG function incorporates optimal scaling and can be used when the predictor(s) and outcome variables are any combination of numeric, ordinal, or nominal. Standard multiple regression can only accommodate an outcome variable which is continuous or nearly continuous (i.e. interval/ratio in scale) and it works best with continuous or nearly continuous predictor variables. Although standard regression can accommodate categorical predictors using one of the following strategies for those types of predictors: dummy coding, effects coding, orthogonal coding, or criterion coding. Binomial Logistic regression is appropriate when the outcome is a dichotomous variable (i.e. categorical with only two categories). Multi-nomial Logistic Regression or Discriminant Function Analysis is appropriate when the outcome variable is polytomous (i.e. categorical with more than two categories).

It is recommended that when conducting categorical regression, one approach the process as one would approach a data reduction process; meaning it is often necessary to conduct multiple runs of the analysis while slightly changing the options / parameters in an effort to discover the best results (i.e. best fitting model and most substantively meaningful interpretation of results).

For the duration of this tutorial we will be using the catreg2.sav file; which contains 1 outcome variable (y) and 5 predictor variables (x1 - x5). The outcome variable was operationally defined as general happiness and was measured with a subjective rating scale. Each of the five predictors were 8-point Likert scaled questionnaire items which are believed to measure preferences for various types of social interactions.

(1) Evaluate the variables.

Begin by conducting a Frequency function to get an idea of how our variables are distributed. Click on Analyze, Descriptive Statistics, Frequencies...

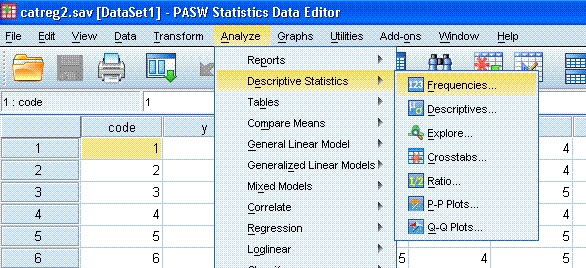
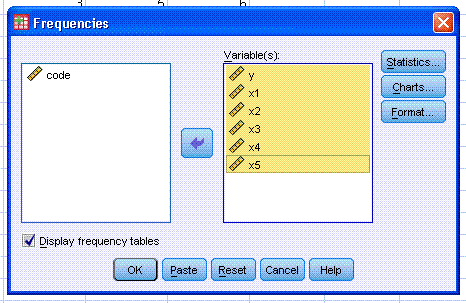
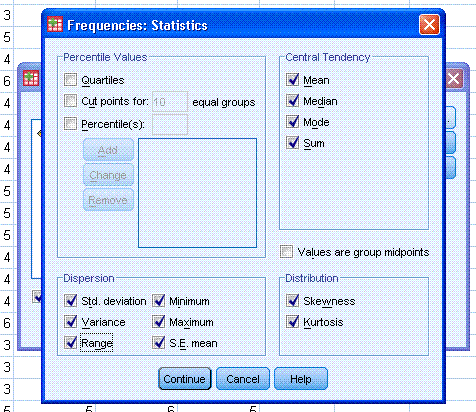
Next, highlight / select all of the variables and use the arrow button to move them to the Variable(s): box. Then click on the Statistics... button and select the following. Then click Continue.

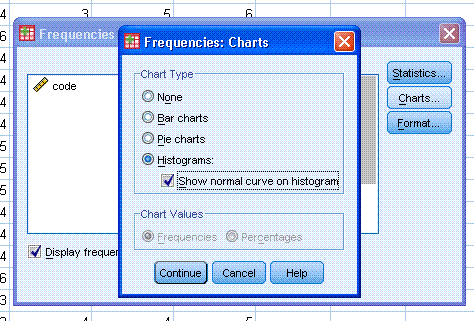
Next, click on the Charts... button, and select, Histograms: and then click the box for Show normal curve on histogram. Then click the Continue button, then click the OK button.

The output should be similar to what is displayed below.

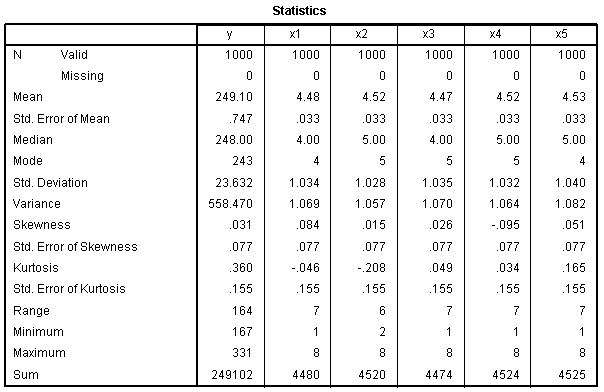
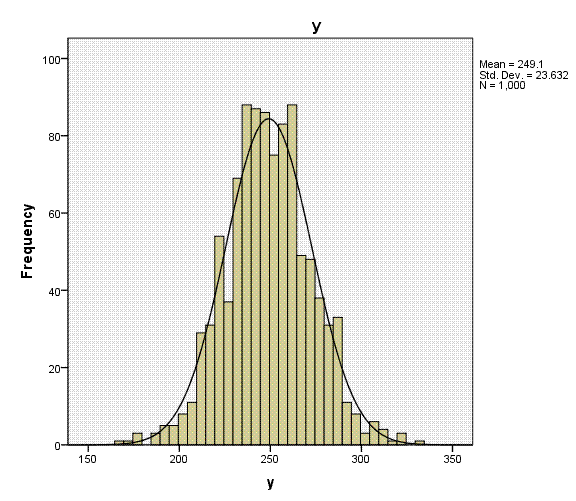
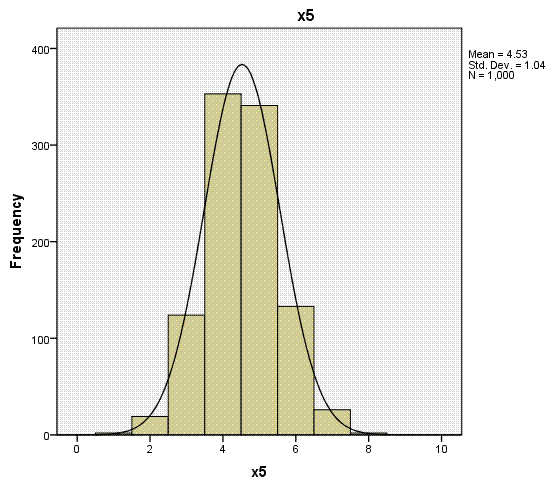
Here, we see that our outcome variable not only has a substantial range of 164 values, but it also has very low values for skewness (.031) and kurtosis (.360) which indicate a fairly normally distributed variable. In fact, we could treat this ordinal variable as numeric or nearly continuous and decide to run a standard multiple regression. But, we would need to use a coding strategy for  the predictor variables if we did choose to run the standard multiple regression. Also, as this example shows, it is better to run a categorical regression on this data because of the opportunity to apply optimal scaling and because all the predictors appear to be and are nominal or ordinal. 

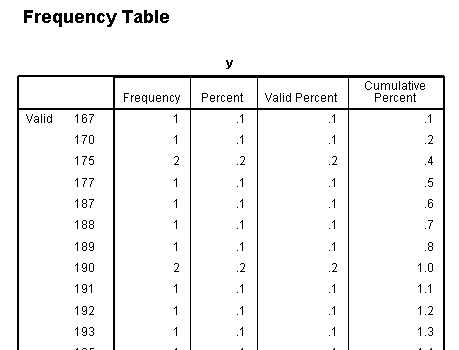
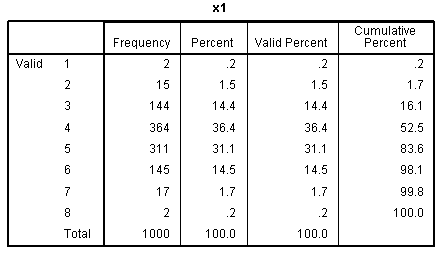
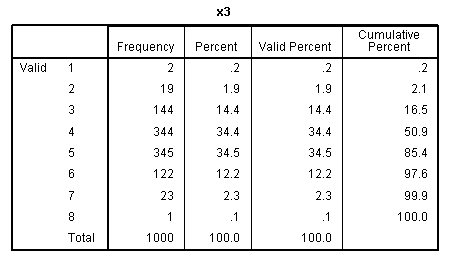
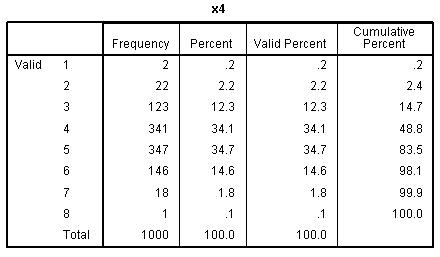
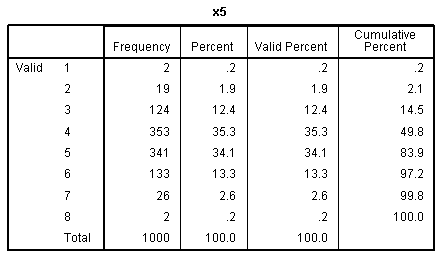
The frequency table for y has been truncated to save space, but it too shows how broadly distributed the values are on our outcome variable. The other frequency tables show the discrete nature of our predictor variables.

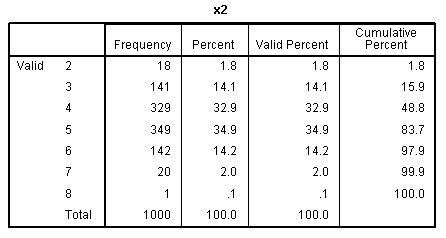
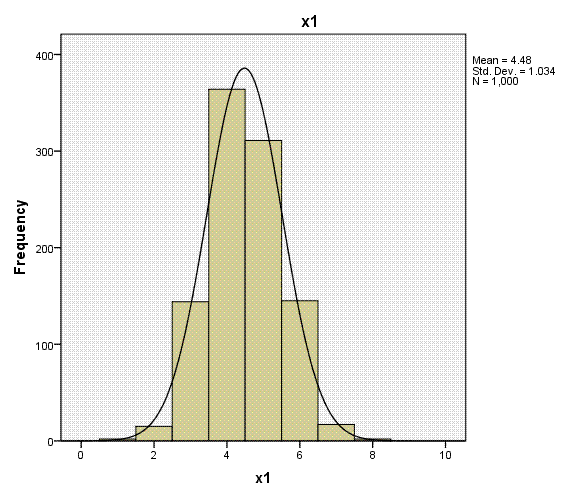
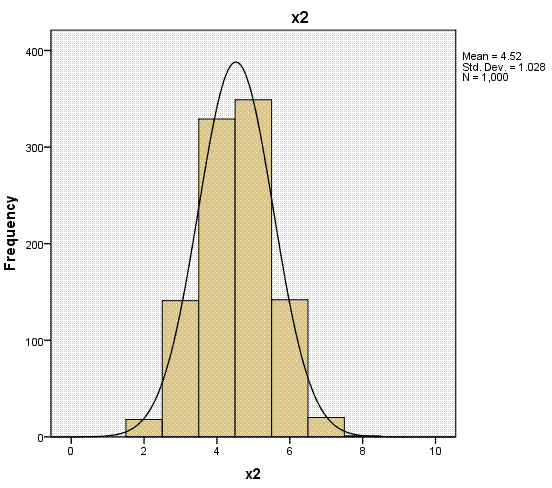
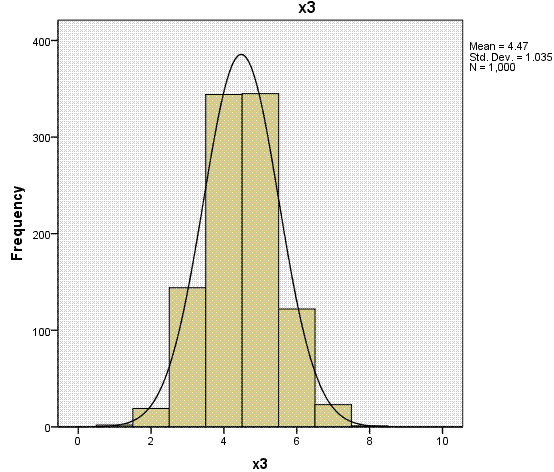
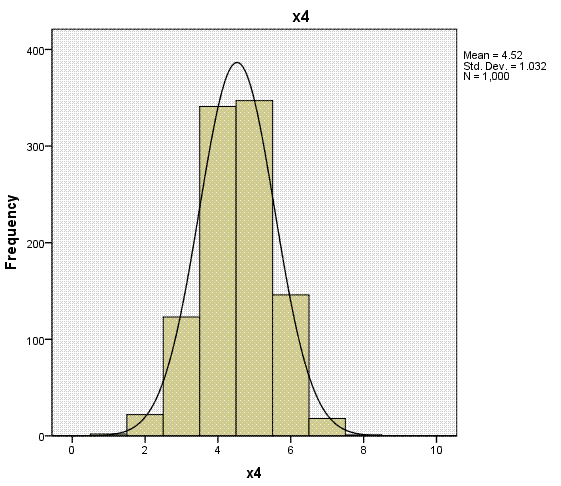
Again, the histogram (with super-imposed normal curves) shows how well our outcome variable (which is nominal) displays the characteristics of an interval or ratio variable. Bar charts would be more appropriate for categorical variables (showing the discrete nature of the variables), but we can see each of the predictors displays narrow range across values 1 - 8.

(2) Standard (multiple) Regression for comparison.

Running a standard multiple regression gives us a baseline model for comparison. Click on Analyze, Regression, Linear...

Next, highlight / select y and use the top arrow button to move it to the Dependent: box. Then, select all the predictors and move them to the Independent(s): box. Then, click the Statistics button.

     Next, select Descriptives (this will produce a Pearson correlation matrix). 

Next, click the Continue button, then click the OK button.

The output should be similar to what is displayed below.

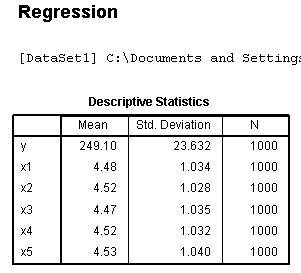
The Descriptive Statistics table shows some of the same information provided in the frequencies function above. The Correlations table provides us with an idea of the relationship between each of the variable. It provides only an idea, because a polychoric correlation matrix (rather than a Pearson correlation matrix) would be more appropriate given the nature of the variables. Pay particular attention to the relationships between each predictor and the outcome variable. Also, notice the lack of multicollinearity (i.e. low magnitude relationships between the predictors). The significance associated with this data is likely to be of little use given the fairly large sample size of the data (N = 1000).

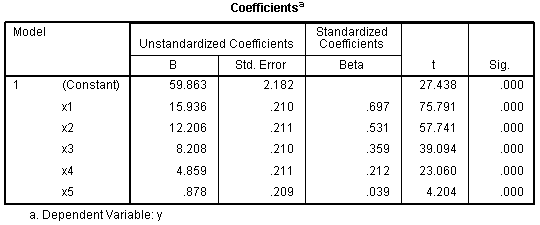
The Variables Entered/Removed table shows just that, all the predictors in the model and none removed. The Model Summary tables shows the multiple correlation coefficient (R?), squared multiple correlation coefficient (R?), adjusted multiple correlation coefficient (adj.R?), and standard error of the estimate. According to our model summary, the collection of predictors accounts for 91.6% (adj.R? = .916) of the variance in our outcome variable.

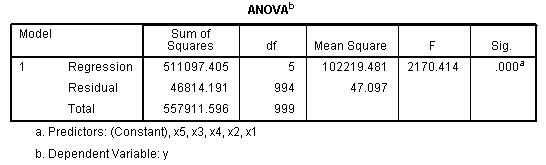
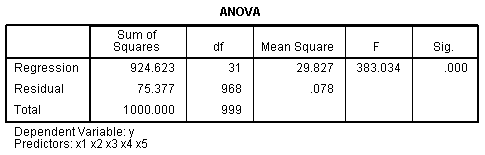
The ANOVA table simply tells us our R? is significantly different from zero. Pay particular attention to the magnitude and order of magnitude of the standardized coefficients or Beta (β)coefficients, for each of our predictors in the Coefficients table. They should be close to the bi-variate correlations for each predictor with the outcome, as listed above in the Correlations table.

(3) First Categorical Regression Analysis.

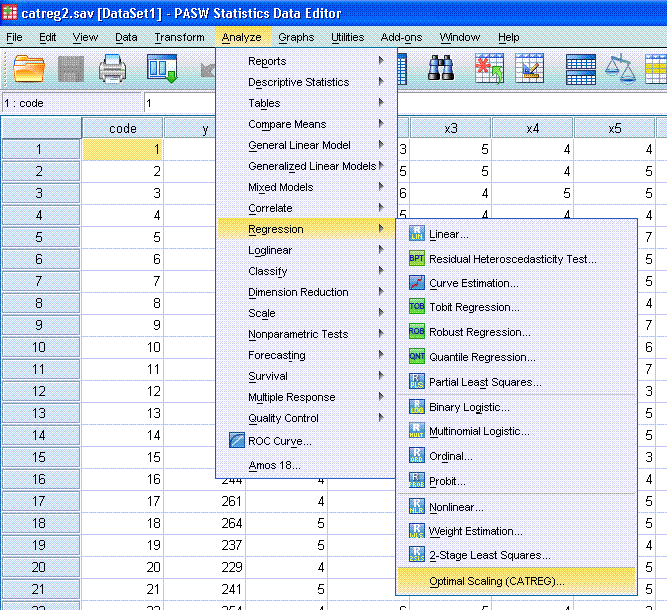
Returning to the Data Window, click on Analyze, Regression, Optimal Scaling (CATREG)...

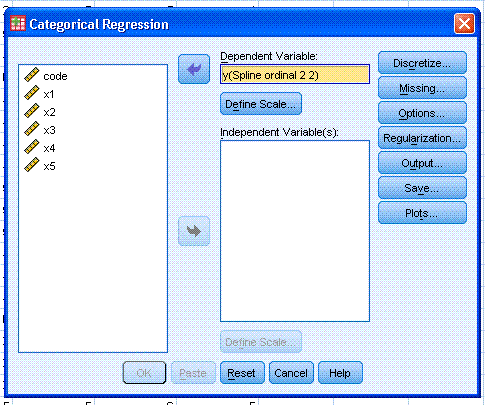
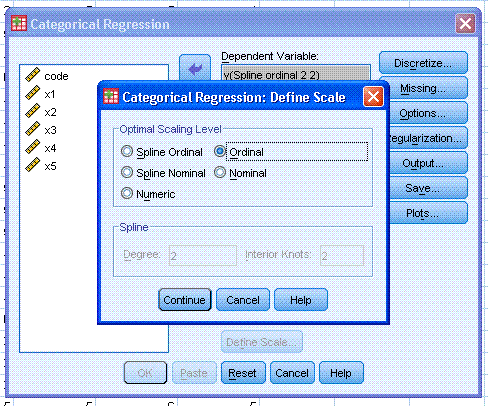
Next, select the outcome variable (y) and use the top arrow button to move it to the Dependent Variable: box. Then, click on the top Define Scale... button and select Ordinal. You can see here the different levels of scale / measurement available. Then, click the Continue button.

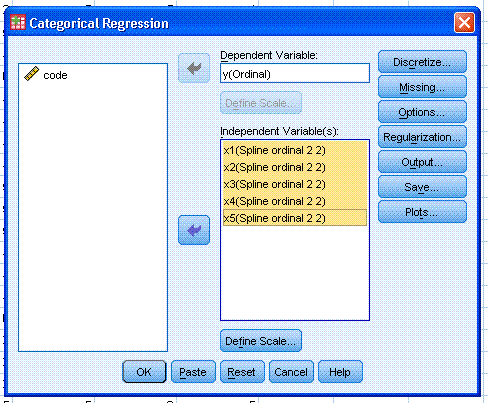
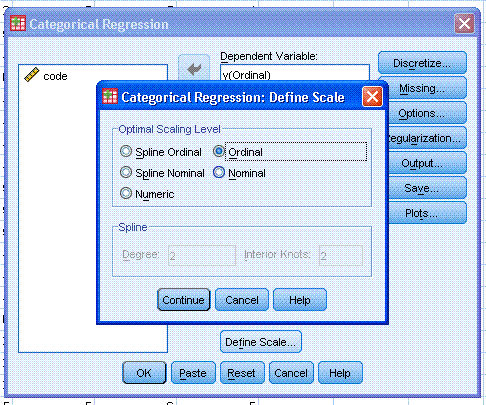
Next, select all 5 predictor variables and use the lower arrow button to move them to the Independent Variable(s): box. Then, click on the lower Define Scale... button and select Ordinal for all 5 predictors. Again, you can see here the different levels of scale / measurement available. Then, click the Continue button.

Next, click on the Output... button and select Correlations of original variables and Correlations of transformed variables. Then click the Continue button. Notice, if you click on the Save... button, you have the ability to save predicted and / or residual values. Next, click the OK button. Keep in mind, the optimal scaling process is iterative and can take a minute or more.

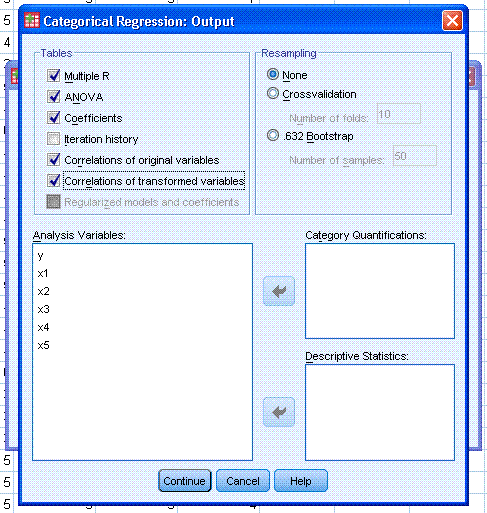
The output should be similar to what is displayed below.

The first two tables are of little to no interest for interpretation; we now know who to thank for inclusion of this analysis in SPSS and there was no missing data.

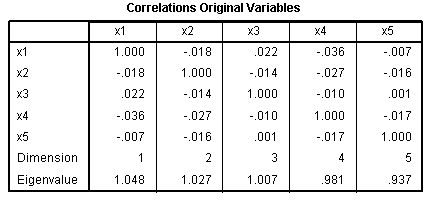
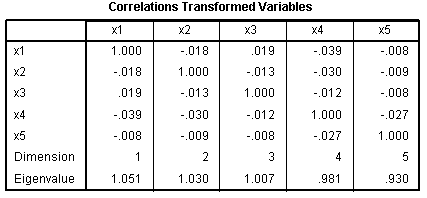
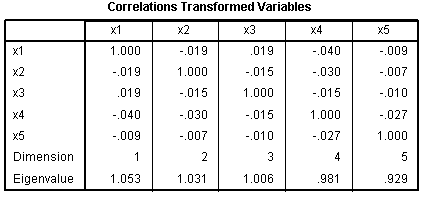
The two correlation tables show the original relationships between the predictor variables (identical to what we saw in the original Correlations table above), and the correlations between our transformed (i.e. optimally scaled) predictor variables. Again, there is no danger of violating the regression assumption of no multicollinearity; meaning, our predictor variables are not substantially related.

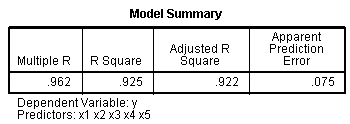
The Model Summary table shows the R, R?, adj.R?, and standard error; all of which are improvements over the standard multiple regression. The R script file used to generate this data can be found here.

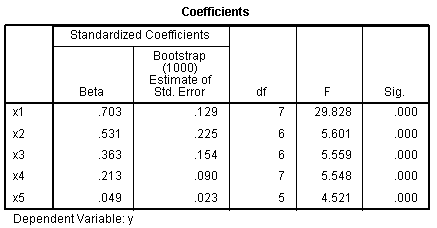
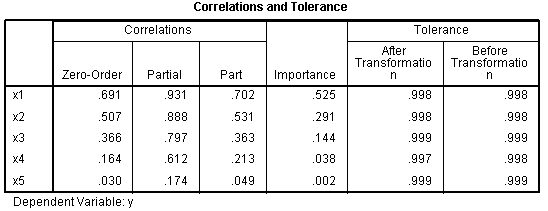
The Coefficients table and the Correlations and Tolerance table display a consistent pattern of relationships between each predictor and the outcome when compared to the correlations and Beta coefficients tables displayed in the standard multiple regression. Focus on the Beta coefficients, zero-order correlations, partial correlations, part correlations (semi-partial), and importance. In these two tables, the strongest predictor is x1; followed by x2, x3, x4, and x5. All of which is consistent with the standard multiple regression and how the data was simulated / generated. 

In pursuit of being thorough, we can run a second CATREG with the outcome variable specified as numeric (which the histogram above suggests is appropriate).

(4) Second Categorical Regression Analysis.

Returning to the Data Window, click on Analyze, Regression, Optimal Scaling (CATREG)...

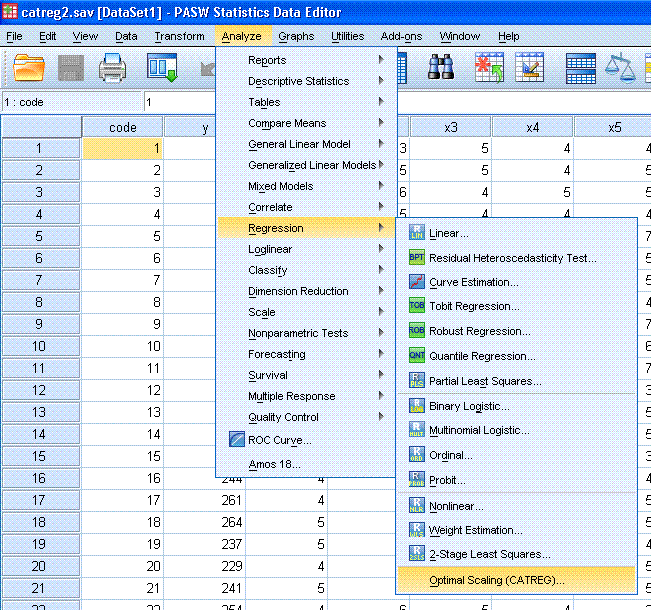
You'll notice the previous run of the analysis is still specified. Here, all we need to do is highlight / select y in the Dependent Variable: box, then click on the Define Scale... button (marked here with a red ellipse).

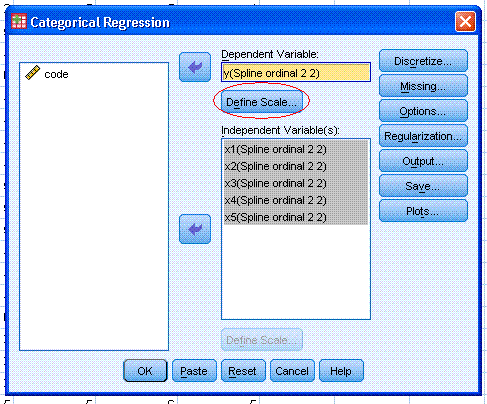
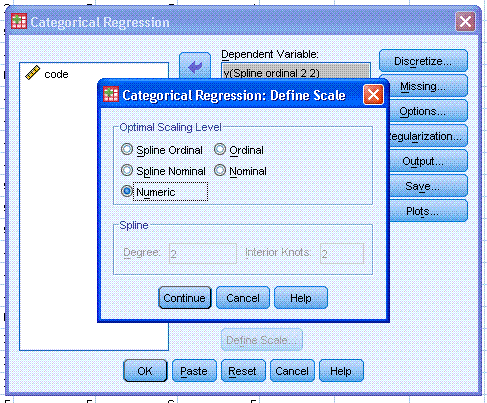
Next, change the scale from Ordinal to Numeric. Then click the Continue button, then click the OK button.

The output should be similar to what is displayed below.

The first two tables are identical to those from the previous run. 

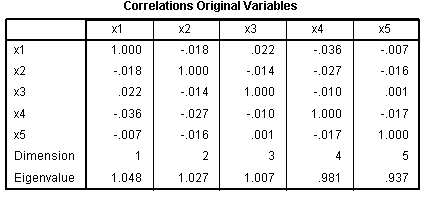
The Correlations Original Variables table is identical to the previous run. The correlations between our transformed (i.e. optimally scaled) predictor variables have changed because of the (newly produced) iterative optimally scaled data. Again, there is no danger of violating the regression assumption of no multicollinearity.

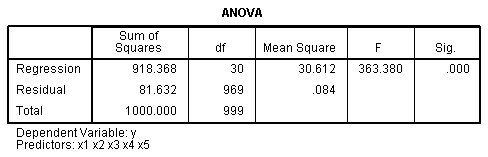
The Model Summary table offers slightly decreased representations of the multiple correlation between all 5 predictors and our outcome variable. The ANOVA table again shows that our R? is significantly different from zero.

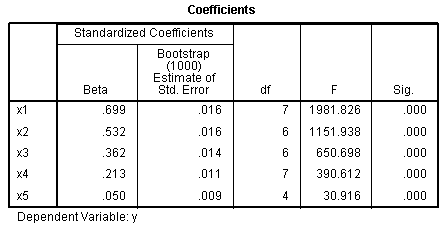
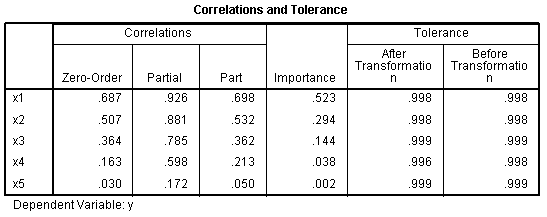
The Coefficients table (Beta coefficients) and the Correlations and Tolerance table (zero-order correlations, partial correlations, part correlations [semi-partial], & importance) show values which  closely resemble the original relationships; but are slightly lower. Whether one chose to report the strictly ordinal results or the current numeric outcome results is a matter of opinion. The ordinal results provide slightly higher estimates of the relationships examined but; the current numeric outcome results may more accurately represent the data, and the difference between the two is negligible.

This should highlight the importance of (1) knowing the operational definitions of variables, (2) conducting initial data analysis (IDA) by running frequencies and / or descriptive statistics functions, and (3) conducting multiple analysis while modifying the options / parameters to extract as much information as possible from the data. Here, the true relationships of the variables are reflected while running either analysis. In this example we knew the true relationships between the variables because we used simulation to generate the data. In a genuine research study, it is recommended one conduct simulation studies in order to more easily recognize the patterns in the data and have confidence in the analysis being performed. However, even if simulation is not used prior to collecting the actual data, one should have at least some understanding of the underlying relationships between the variables of interest based on a thorough literature review (i.e. prior research and theory associated with the area of study).

REFERENCES and RESOURCES

de Leeuw, J. (1988). Multivariate analysis with linearizable regressions. Psychometrika, 53(4), 437 - 454. (here).

Meulman, J. J. (1998). Optimal scaling methods for multivariate categorical data analysis. SPSS White Paper, SPSS Inc. (here).

SPSS Content Guideline for CATREG in PASW 18. (here).

Van Der Geer, J. P. (1993). Multivariate analysis of categorical data: Theory. Advanced Quantitative Techniques in the Social Sciences Series (Vol. 2). Sage Publications, Inc.

Van Der Geer, J. P. (1993). Multivariate analysis of categorical data: Applications. Advanced Quantitative Techniques in the Social Sciences Series (Vol. 3). Sage Publications, Inc.

Return to the SPSS Short Course