|
Principal
Components Analysis
in SPSS.
Before we begin with the analysis; let's take a
moment to address and hopefully clarify one of the most confusing and
misarticulated issues in statistical teaching and practice
literature.
First, Principal Components Analysis (PCA)
is a variable reduction technique which maximizes the amount of
variance accounted for in the observed variables by a smaller group of
variables called COMPONENTS. As an example, consider the following
situation. Let's say, we have 500 questions on a survey we designed to
measure persistence. We want to reduce the number of questions so that
it does not take someone 3 hours to complete the survey. It would be
appropriate to use PCA to reduce the number of questions by identifying
and removing redundant questions. For instance, if question 122 and
question 356 are virtually identical (i.e. they ask the exact same
thing but in different ways), then one of them is not necessary. The
PCA process allows us to reduce the number of questions or variables
down to their PRINCIPAL COMPONENTS.
PCA is commonly, but very confusingly, called
exploratory factor analysis (EFA). The use of the word factor
in EFA is inappropriate and confusing because we are really interested
in COMPONENTS, not factors. This issue is made more confusing by some
software packages (e.g. PASW/SPSS & SAS) which list or use PCA
under the heading factor analysis.
Second, Factor Analysis (FA) is
typically used to confirm the latent factor structure for a group of
measured variables. Latent factors are unobserved variables which
typically can not be directly measured; but, they are assumed to cause
the scores we observe on the measured or indicator variables. FA is a
model based technique. It is concerned with modeling the relationships
between measured variables, latent factors, and error.
As stated in O'Rourke, Hatcher, and Stepanski
(2005): "Both (PCA & FA) are methods that can be used to
identify groups of observed variables that tend to hang together
empirically. Both procedures can also be performed with the SAS FACTOR
procedure and they generally tend to provide similar results.
Nonetheless, there are some important conceptual differences between
principal component analysis and factor analysis that should be
understood at the outset. Perhaps the most important deals with the
assumption of an underlying causal structure. Factor analysis assumes
that the covariation in the observed variables is due to the presence
of one or more latent variables (factors) that exert causal influence
on these observed variables" (p. 436).
Final thoughts. Both PCA and FA can be used as
exploratory analysis. But; PCA is predominantly used in an exploratory
fashion and almost never used in a confirmatory fashion. FA can be used
in an exploratory fashion, but most of the time it is used in a
confirmatory fashion because it is concerned with modeling factor
structure. The choice of which is used should be driven by the goals of
the analyst. If you are interested in reducing the observed variables
down to their principal components while maximizing the variance
accounted for in the variables by the components, then you should be
using PCA. If you are concerned with modeling the latent factors (and
their relationships) which cause the scores on your observed variables,
then you should be using FA.
Principal Components Analysis
The following covers a few of the SPSS procedures
for conducting principal component analysis. For the duration of this
tutorial we will be using the
ExampleData4.sav
file.
PCA 1. So,
here we go. Begin by clicking on Analyze, Dimension Reduction, Factor...
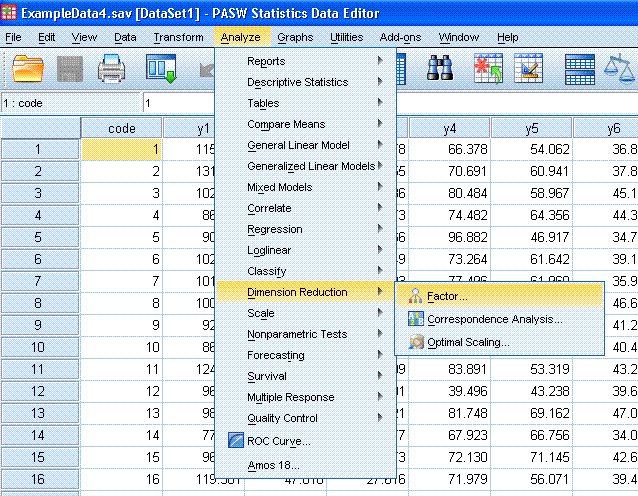
Next, highlight all the variables you want to
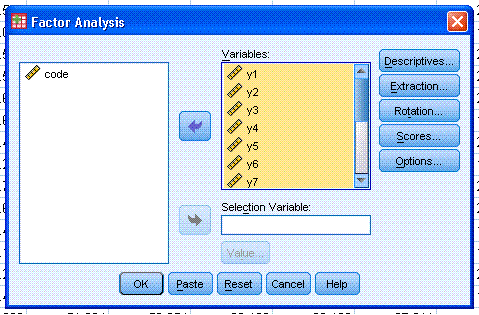
include in the analysis; here y1 through y15. Then click on
Descriptives...and select the following. Then click the Continue
button.
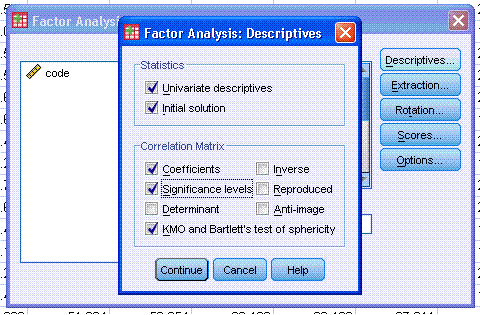
Next, click on the Extraction... button and select
the following (notice Principal components is specified by default).
Also notice the extraction is based on components with eigenvalues
greater than 1 (also a default). There are a number of perspectives on
determining the number of components to extract and what criteria to
use for extraction. Originally, eigenvalues greater than 1 was
generally accepted. However, more recently
Zwick
and Velicer (1986) have suggested, Horn’s (1965) parallel analysis
tends to be more precise in determining the number of reliable
components or factors. Unfortunately, Parallel Analysis is not
available in SPSS. Therefore, a review of the parallel analysis engine (Patil, Singh, Mishra,
& Donavan, 2007) is strongly recommended. Next,
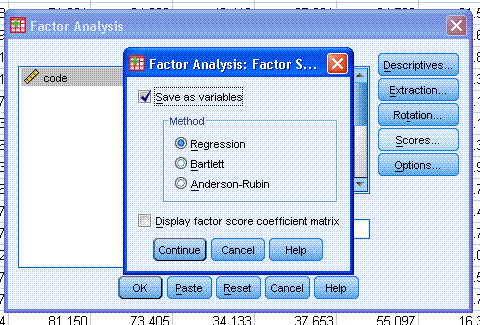
click the Continue button, then click the Scores... button.
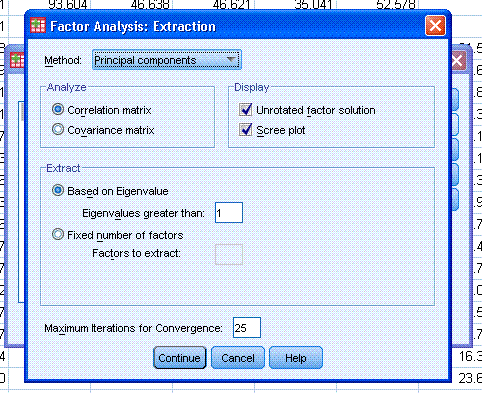
Scores... will add new columns to our dataset; each new column will
consist of each variable's score on each extracted component. Then,
click on the Continue button, then click the OK button.
The output should be similar to what is displayed
below.
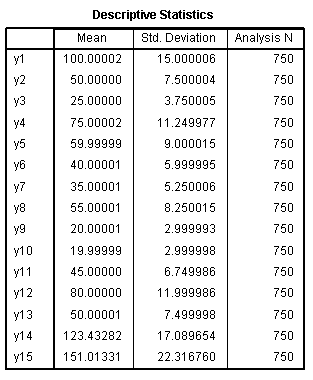 The Descriptive Statistics
table simply reports the mean, standard deviation, and number of cases
for each variable included in the analysis. The Descriptive Statistics
table simply reports the mean, standard deviation, and number of cases
for each variable included in the analysis.
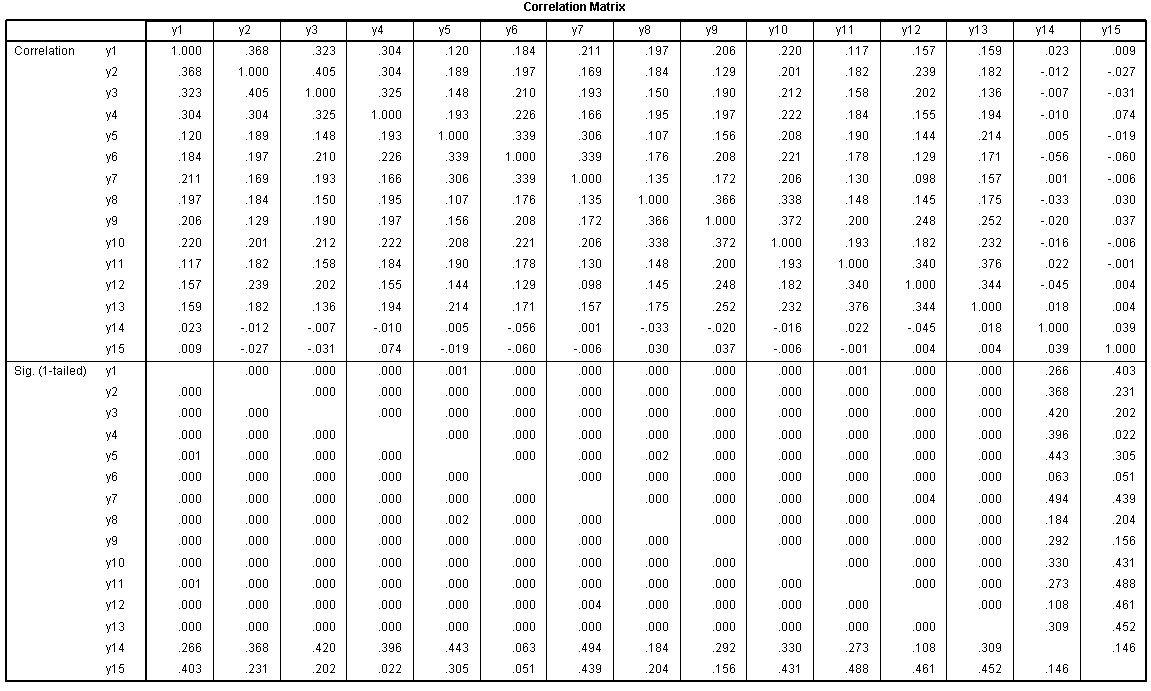
The Correlation Matrix (above) is the correlation
matrix for the variables included. Generally speaking, a close review
of this table can offer an insight into how the PCA results will come
out.

The next table is used as to test assumptions;
essentially, the Kaiser-Meyer-Olking (KMO) statistic should be greater
than 0.600 and the Bartlett's test should be significant (e.g. p
< .05). KMO is used for assessing sampling
adequacy and evaluates the correlations and partial correlations to
determine if the data are likely to coalesce on components (i.e. some
items highly correlated, some not). The Bartlett's test evaluates
whether or not our correlation matrix is an identity matrix (1 on the
diagonal & 0 on the off-diagonal). Here, it indicates that our
correlation matrix (of items) is not an identity matrix--we can verify
this by looking at the correlation matrix. The off-diagonal values of
our correlation matrix are NOT zeros, therefore the matrix is NOT an
identity matrix.
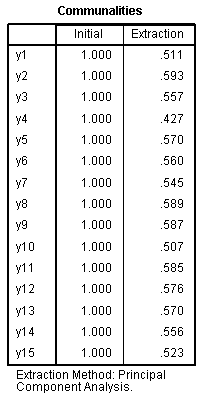
A communality (h?) is the sum of the
squared component loadings and represents the amount of variance in
that variable accounted for by all the components. For example, all
five extracted components account for 51.1% of the variance in variable
y1 (h? =
.511).
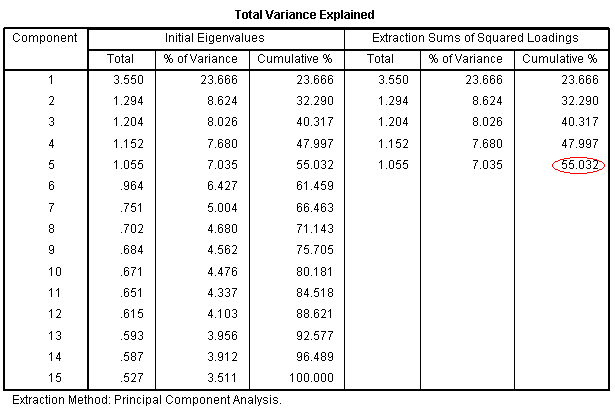
The next table is intuitively named and reports
the variance explained by each component as well as the cumulative
variance explained by all components. When we speak of variance
explained with regard to this table, we are referring to the amount of
variance in the total collection of variables/items which is explained
by the component(s). For instance, component 5 explains 7.035% of the
variance in the items; specifically, in the items' variance-covariance
matrix. We could also say, 55.032% of the variance in our items was
explained by the 5 extracted components.
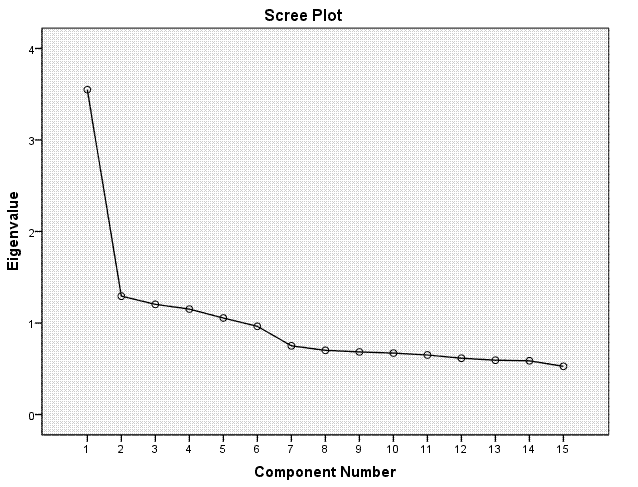
The scree plot graphically displays the
information in the previous table; the components' eigenvalues.
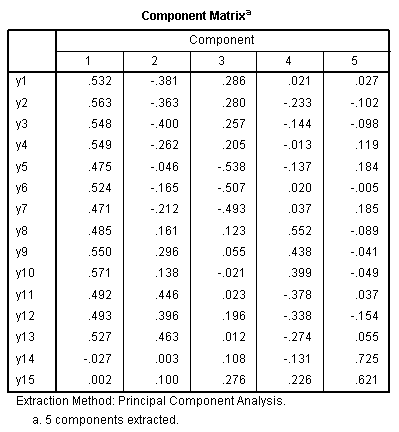
The next table displays each variable's loading on
each component. We notice from the output, we have two items (y14
& y15) which do not load on the first component (always the
strongest component without rotation) but create their own retained
component (also with eigenvalue greater than 1). We know a component
should have, as a minimum, 3 items/variables; but let's reserve
deletion of items until we can discover whether or not our components
are related.
To determine if our components are related, we can
run a simple correlation on the saved component scores. Click on
Analyze, Correlate, Bivariate...

Next, highlight all the REGR factor scores (really
component scores) and use the arrow button to move them to the
Variables: box. Then click the OK button.
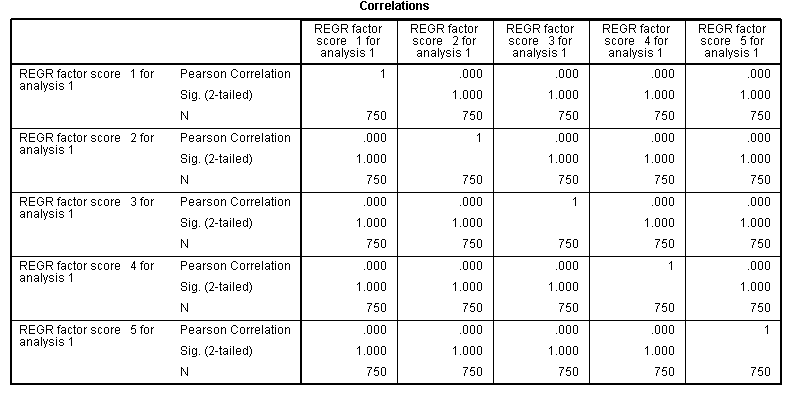
Here we see there is NO relationship between the
components; which indicates we should be using an orthogonal rotation
strategy.
PCA 2.
Rotation imposed. Next, we re-run the PCA specifying 5 components to be
retained. We will also specify the VARIMAX rotation strategy, which is
a form of orthogonal rotation.
Begin by clicking on Analyze, Dimension Reduction,
Factor...

Next, you should see that the previous run is
still specified; variables y1 through y15. Next click on
Descriptives...and select the following; we no longer need the
univariate descriptives, the correlation matrix, or the KMO and
Bartlett's tests. Then click the Continue button. Next, click on the
Extraction... button. We no longer need the scree plot; but we do need
to change the number of components (here called factors) to extract. We
know from the first run, there were 5 components with eigenvalues
greater than one, so we select 5 factors to extract (meaning
components). Then click the Continue button.
Next, click on Rotation... and select Varimax.
Then click the Continue button. Then click on the Scores... button and
remove the selection for Save as Variables. Then click the Continue
button. Then click the OK button.
The first 3 tables in the output should be
identical to what is displayed above from PCA 1; accept, now we have
two new tables at the bottom of the output.
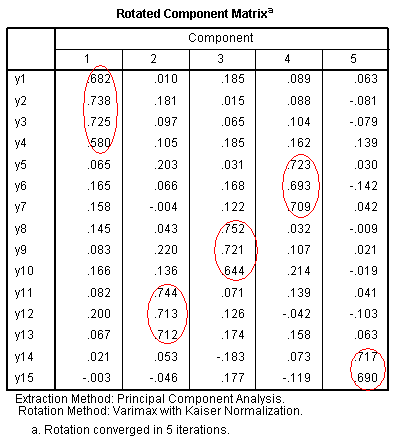
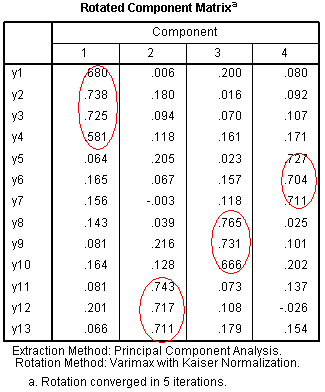
The rotated component matrix table shows which
items/variables load on which components after rotation. We see that
the rotation cleaned up the interpretation by eliminating the global
first component. This provides a clear depiction of our principal components (marked
with red ellipses).
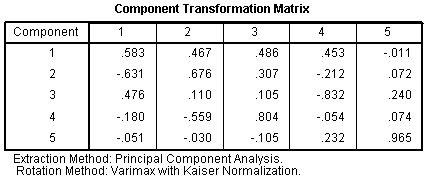
The Component Transformation Matrix simply
displays the component correlation matrix prior to and after rotation.
PCA 3.
Finally, we can eliminate the two items (y14 & y15) which (a)
by themselves create a component (components should have more than 2
items or variables) and (b) do not load on the un-rotated or initial
component 1. Again, click on Analyze, Dimension Reduction, then
Factor...

Again, you'll notice the previous run is still
specified, however we need to remove the y14 and y15 variables. Next,
click on Extraction... and change the number of factors to extract
(really components) from 5 to 4. Then click the Continue button and
then click the OK button.
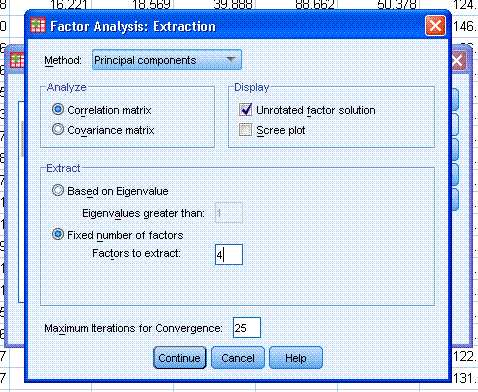
The output should be similar to what is displayed
below.
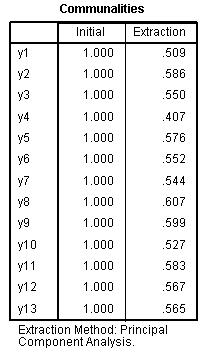
All the communalities indicate 50% or more of
the variance in each variable/item is explained by the combined four
components; with one exception (y4) which is lower than what we would
prefer.
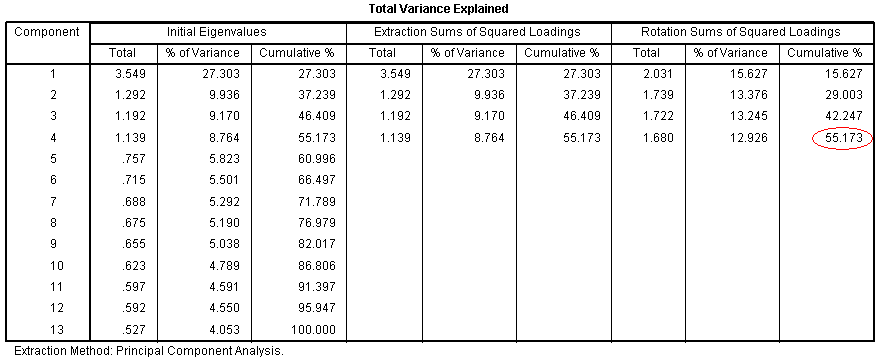
The Component Matrix table displays component
loadings for each item (prior to rotation).
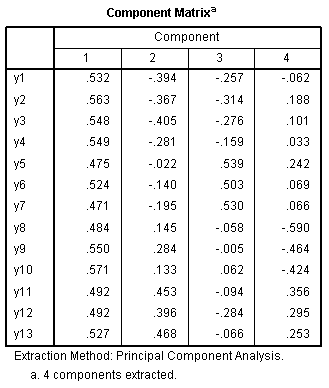 The
Rotated Component Matrix displays the loadings for each item on each
rotated component, again clearly showing which items make up each
component. The
Rotated Component Matrix displays the loadings for each item on each
rotated component, again clearly showing which items make up each
component.
And again, the Component Transformation Matrix
displays the correlations among the components prior to and after
rotation.

To help clarify the purpose of PCA, consider
reviewing the table with the title "Total Variance Explained" from PCA
1. The last column on the right in that table is called
"Cumulative" and refers to the cumulative variance accounted for by the
components. Now focus on the fifth value from the top in that column.
That value of 55.032 tells us 55.032% of the variance in the items
(specifically the items' variance - covariance matrix) is accounted for
by all 5 components. As a comparison, and to highlight the purpose of
PCA; look at the same table only for PCA 3, which
has the title "Total Variance Explained". Pay particular attention to
the fourth value in the last (cumulative) column. This value of 55.173
tells us 55.173% of the variance in the items (specifically the items'
variance - covariance matrix) is accounted for by all 4 components. So,
we have reduced the number of items from 15 to 13, reduced the number
of components, and yet have improved the amount of variance accounted
for in the items by our principal components.
REFERENCES / RESOURCES
Horn, J. (1965). A rationale and test for the number of factors in
factor analysis. Psychometrika, 30, 179 – 185.
O'Rourke, N., Hatcher, L., & Stepanski,
E.J. (2005). A step-by-step approach to using SAS for univariate and
multivariate statistics, Second Edition. Cary, NC: SAS Institute Inc.
Patil,
V. H.,
Singh, S. N., Mishra, S., &
Donavan, D. T. (2007). Parallel Analysis Engine to Aid Determining
Number of Factors to Retain [Computer software]. Retrieved 08/23/2009
from
http://ires.ku.edu/~smishra/parallelengine.htm
Zwick, W. R., & Velicer, W. F. (1986). Factors influencing five
rules for determing the number of components to retain. Psychological
Bulletin, 99,
432 – 442.
|


